Case Study in R: How Does a Bike-Share Navigate Speedy Success

IV. Data Cleaning in R

Pre-requisites

Dataframe names:

• df_trips_YYYYMM: raw data input for each month
  
• df_trips_all_raw: merged data of all months
  
• df_trips_all_clean_xxx: cleaned data
  
• df_trips_all_trans: added columns for duration, weekdays, hours
  
• df_trips_all_fct: format categorical variables into factors
  
• df_trips_all_final: removed outliers
  
• df_trips_all_final_dense: removed non essential columns
  
  

Install and load packages:

library(tidyverse)
library(lubridate)
library(here)
library(gridExtra)
library(sf)

1 Importing raw data

1.1 Importing data

Datasets

Please download the following data files from the [Link] (https://divvy-tripdata.s3.amazonaws.com/index.html) and copy them into your working directory “data” of RStudio

Data set: ‘202201-divvy-tripdata.csv’ (data for one month Jan. 2022)
Data set: ‘202202-divvy-tripdata.csv’ (data for one month Feb. 2022)
Data set: ‘202203-divvy-tripdata.csv’ (data for one month Mar. 2022)
Data set: ‘202204-divvy-tripdata.csv’ (data for one month Apr. 2022)
Data set: ‘202205-divvy-tripdata.csv’ (data for one month May. 2022)
Data set: ‘202206-divvy-tripdata.csv’ (data for one month Jun. 2022)
Data set: ‘202207-divvy-tripdata.csv’ (data for one month Jul. 2022)
Data set: ‘202208-divvy-tripdata.csv’ (data for one month Aug. 2022)
Data set: ‘202209-divvy-tripdata.csv’ (data for one month Sep. 2022)
Data set: ‘202210-divvy-tripdata.csv’ (data for one month Oct. 2022)
Data set: ‘202211-divvy-tripdata.csv’ (data for one month Nov. 2022)
Data set: ‘202212-divvy-tripdata.csv’ (data for one month Dec. 2022)

Reading 12 CSV files into separated dataframes from the local storage:

# ------------------------------------------------------------ set wd with here
file_202201 <- here("data", "202201-divvy-tripdata.csv")
file_202202 <- here("data", "202202-divvy-tripdata.csv")
file_202203 <- here("data", "202203-divvy-tripdata.csv")
file_202204 <- here("data", "202204-divvy-tripdata.csv")
file_202205 <- here("data", "202205-divvy-tripdata.csv")
file_202206 <- here("data", "202206-divvy-tripdata.csv")
file_202207 <- here("data", "202207-divvy-tripdata.csv")
file_202208 <- here("data", "202208-divvy-tripdata.csv")
file_202209 <- here("data", "202209-divvy-tripdata.csv")
file_202210 <- here("data", "202210-divvy-tripdata.csv")
file_202211 <- here("data", "202211-divvy-tripdata.csv")
file_202212 <- here("data", "202212-divvy-tripdata.csv")


# ------------------------------------------------------------------ read files
df_trips_202201 <- read_csv(file_202201)
df_trips_202202 <- read_csv(file_202202)
df_trips_202203 <- read_csv(file_202203)
df_trips_202204 <- read_csv(file_202204)
df_trips_202205 <- read_csv(file_202205)
df_trips_202206 <- read_csv(file_202206)
df_trips_202207 <- read_csv(file_202207)
df_trips_202208 <- read_csv(file_202208)
df_trips_202209 <- read_csv(file_202209)
df_trips_202210 <- read_csv(file_202210)
df_trips_202211 <- read_csv(file_202211)
df_trips_202212 <- read_csv(file_202212)

# ------------------------------------------------------------------- clean up
rm(file_202201,
   file_202202,
   file_202203,
   file_202204,
   file_202205,
   file_202206,
   file_202207,
   file_202208,
   file_202209,
   file_202210,
   file_202211,
   file_202212
   )

1.2 Union data

Next we will merge all 12 dataframes into one single dataframe with all the raw data.

# ------------------------------------------ union all files into one data frame
df_trips_all_raw <- df_trips_202201 %>% 
  union_all(df_trips_202202) %>% 
  union_all(df_trips_202203) %>%
  union_all(df_trips_202204) %>%
  union_all(df_trips_202205) %>%
  union_all(df_trips_202206) %>%
  union_all(df_trips_202207) %>%
  union_all(df_trips_202208) %>%
  union_all(df_trips_202209) %>%
  union_all(df_trips_202210) %>% 
  union_all(df_trips_202211) %>% 
  union_all(df_trips_202212)

# ---------------------------------------------------------- remove single files
rm(df_trips_202201,
   df_trips_202202,
   df_trips_202203,
   df_trips_202204,
   df_trips_202205,
   df_trips_202206,
   df_trips_202207,
   df_trips_202208,
   df_trips_202209,
   df_trips_202210,
   df_trips_202211,
   df_trips_202212
)

Result:

• Numbers of rows: 5,667,717
  
• Numbers of columns: 13
  
  

2. Cleaning the data

2.1 Check data integrity

2.1.1 Check numbers of NAs

colSums(is.na(df_trips_all_raw)) %>% 
  data.frame() %>% 
  print()

##                         .
## ride_id                 0
## rideable_type           0
## started_at              0
## ended_at                0
## start_station_name 833064
## start_station_id   833064
## end_station_name   892742
## end_station_id     892742
## start_lat               0
## start_lng               0
## end_lat              5858
## end_lng              5858
## member_casual           0

Result:

• About 1.7 million start or end station names are missing.
  
• Geo-codes are mostly available. However, the reconstruction of station names from geo-codes would require a more deep-dive into map-matching and is out of the scope of this project. We, therefore have to remove all rows with NAs, which is acceptable since we still have about 75% of data left.
  

2.1.2 Check time range

df_trips_all_raw %>% 
  summarise(
    min_start = min(started_at), 
    max_start = max(started_at),
    min_end = min(ended_at), 
    max_end = max(ended_at)) %>% 
  pivot_longer(cols = 1:4,
               names_to = "station",
               values_to = "time range") %>% 
  print()

## # A tibble: 4 × 2
##   station   `time range`       
##   <chr>     <dttm>             
## 1 min_start 2022-01-01 00:00:05
## 2 max_start 2022-12-31 23:59:26
## 3 min_end   2022-01-01 00:01:48
## 4 max_end   2023-01-02 04:56:45

Result:

• max end datetime exceeded by two days (2023-01-02). This will be cleaned in the outlier removal step
  
  

2.1.3 Check for time dependency issues

df_trips_all_raw %>% 
  filter(started_at > ended_at) %>% 
  summarise(n_time_conflict = n())

## # A tibble: 1 × 1
##   n_time_conflict
##             <int>
## 1             100

Result:

• There are 100 observations with a time conflict. These rows will be removed.
  
  

2.1.4 Check distinct values

df_trips_all_raw %>% 
  summarise(n_bike_type = n_distinct(rideable_type),
            n_user = n_distinct(member_casual),
            n_start_station = n_distinct(start_station_name),
            n_end_station = n_distinct(end_station_name)) %>% 
  pivot_longer(cols = 1:4,
               names_to = "variables",
               values_to = "distinct count")

## # A tibble: 4 × 2
##   variables       `distinct count`
##   <chr>                      <int>
## 1 n_bike_type                    3
## 2 n_user                         2
## 3 n_start_station             1675
## 4 n_end_station               1693

Result:

• Distinct numbers of bike types (3) and users (2) are plausible
  
• Distinct number of start and end station (1693) is exceeding the amount of stated 600 docking stations. The stations listed in the dataset may include different names for the same docking station as well as non-docking locations. Since we have no further information, we will treat all 1693 stations as valid.
  
  

2.1.5 Check for location outliers

Create a dataframe for stations:

# -------------------------------------------------------- df for start stations 
df_start_stations <- df_trips_all_raw %>%
  select(start_station_name, start_lat, start_lng) %>% 
  filter(!is.na(start_station_name) & !is.na(start_lat) & !is.na(start_lng)) %>% 
  group_by(start_station_name) %>% 
  summarise(latitude = mean(start_lat),
            longitude = mean(start_lng)) %>%
  select(station_name = start_station_name, latitude, longitude) %>% 
  distinct()

# -------------------------------------------------------- df for start stations 
df_end_stations <- df_trips_all_raw %>%
  select(end_station_name, end_lat, end_lng) %>% 
  filter(!is.na(end_station_name) & !is.na(end_lat) & !is.na(end_lng)) %>% 
  group_by(end_station_name) %>% 
  summarise(latitude = mean(end_lat),
            longitude = mean(end_lng)) %>% 
  select(station_name = end_station_name, latitude, longitude) %>% 
  distinct() 

# -------------------------------------------------------- df all stations
df_stations <- df_start_stations %>% 
  union(df_end_stations)

rm(df_start_stations, df_end_stations)

Plot station location as virtual map:

# --------------------------------------------------------- plot all stations
locations <- st_as_sf(df_stations, coords = c("longitude", "latitude")) 

pl1 <- ggplot(locations) +
  geom_sf(aes()) + 
  labs(title = "All stations")

# ----------------------------------- create plot for Greater Chicago Area (GCA)
df_stations_gta <- df_stations %>% 
  filter((longitude > -90 & longitude < -87) &
         (latitude < 44 & latitude > 40))

locations_gta <- st_as_sf(df_stations_gta, coords = c("longitude", "latitude")) 

pl2 <- ggplot(locations_gta) +
  geom_sf(aes()) + 
  labs(title = "Stations GCA")

# ------------------------------------------------------=--------- arrange plots
grid.arrange(pl2, pl1, ncol = 2)

rm(locations, locations_gta, df_stations, df_stations_gta, pl1, pl2)

There are stations far from Chicago area, probably testing stations. We will neglect these stations and set the area boundary of GCA to:

• Longitude : [-88.0, -87.0]
  
• Latitude : [41.4, 42.4]
  
  

The following stations are identified as outliers:

lng_max <- -87
lng_min <- -88
lat_max <- 42.4
lat_min <- 41.4

df_trips_all_raw %>%
  filter(!(between(end_lng, lng_min, lng_max) & 
          between(end_lat, lat_min, lat_max) &
          between(start_lng, lng_min, lng_max) &
          between(start_lat, lat_min, lat_max)))  %>%
  select(start_station_name, start_lat, start_lng, end_station_name, end_lat, end_lng)

## # A tibble: 11 × 6
##    start_station_name                    start…¹ start…² end_s…³ end_lat end_lng
##    <chr>                                   <dbl>   <dbl> <chr>     <dbl>   <dbl>
##  1 Pawel Bialowas - Test- PBSC charging…    45.6   -73.8 Pawel …    41.9   -87.7
##  2 Dearborn St & Adams St                   41.9   -87.6 <NA>       41.9   -88.1
##  3 Public Rack - Central Ave & North Ave    41.9   -87.8 <NA>       41.9   -88.0
##  4 Franklin St & Adams St (Temp)            41.9   -87.6 Green …     0       0  
##  5 Laflin St & Cullerton St                 41.9   -87.7 Green …     0       0  
##  6 Canal St & Adams St                      41.9   -87.6 Green …     0       0  
##  7 Morgan St & Polk St                      41.9   -87.7 Green …     0       0  
##  8 Aberdeen St & Randolph St                41.9   -87.7 Green …     0       0  
##  9 Green St & Madison St                    41.9   -87.6 Green …     0       0  
## 10 LaSalle St & Jackson Blvd                41.9   -87.6 Green …     0       0  
## 11 Green St & Washington Blvd               41.9   -87.6 Green …     0       0  
## # … with abbreviated variable names ¹​start_lat, ²​start_lng, ³​end_station_name

11 stations are outside of greater Chicago area. They will be removed in the later cleaning process.

2.2 Cleaning the data

2.2.1 Remove NAs

There are plenty of rows with missing values, related to missing recordings of start and end stations. All rows with NAs will be removed.

Remove rows with missing values:

df_trips_all_clean_na <- df_trips_all_raw %>% 
  filter(!(is.na(ride_id) | 
           is.na(rideable_type) | 
           is.na(started_at) |
           is.na(ended_at) | 
           is.na(start_station_name) | 
           is.na(start_station_id) | 
           is.na(end_station_name) | 
           is.na(end_station_id) | 
           is.na(start_lat) | 
           is.na(start_lng) | 
           is.na(end_lat) |
           is.na(end_lng) |
           is.na(member_casual))
  )
rm(df_trips_all_raw)

Result:

• Number of rows removed (with NAs): 1,298,357 (23%)
  
• Number of rows remaining (no NAs): 4,369,360
  
  
  

2.2.2 Remove service stations:

Service stations for maintenance or charging tests should be removed from the dataset. Our first guess was that they can be identified by their long station ID names. However, it turned out that some docking stations with charging devices for electric bikes have long ID names as well. After a review of the 1600 station IDs we identified the following service station names:

• station IDs with name “Pawel Bialowas - Test- PBSC charging station” (length 44)
  
• station IDs with name “DIVVY CASSETTE REPAIR MOBILE STATION” (length 36)
  
• station IDs with name “Hubbard Bike-checking (LBS-WH-TEST)” (length 35)
  
• station IDs with name “DIVVY 001 - Warehouse test station” (length 34)
  
• station IDs with name “2059 Hastings Warehouse Station” (length 31)
  
• station IDs with name “Divvy Valet - Oakwood Beach” (length 27)
  
• station IDs with name “Hastings WH 2” (length 13)
  

# remove service stations 
df_trips_all_clean_serv <- df_trips_all_clean_na %>% 
     filter(!(str_detect(start_station_id, "Pawel Bialowas") |
          str_detect(start_station_id, "DIVVY CASSETTE") |
          str_detect(start_station_id, "Hubbard") |
          str_detect(start_station_id, "DIVVY 001") |
          str_detect(start_station_id, "2059 Hastings") |
          str_detect(start_station_id, "Divvy Valet") |
          str_detect(start_station_id, "Hastings WH") |

          str_detect(end_station_id, "Pawel Bialowas") |
          str_detect(end_station_id, "DIVVY CASSETTE") |
          str_detect(end_station_id, "Hubbard") |
          str_detect(end_station_id, "DIVVY 001") |
          str_detect(end_station_id, "2059 Hastings") |
          str_detect(end_station_id, "Divvy Valet") |
          str_detect(end_station_id, "Hastings WH"))
  )
rm(df_trips_all_clean_na)

Result:

• Removed number of rows with service stations: 1,507
  
• Remaining number of rows: 4,367,853
  
  
  

2.2.3 Remove location outliers

lng_max <- -87
lng_min <- -88
lat_max <- 42.4
lat_min <- 41.4

df_trips_all_clean_serv <- df_trips_all_clean_serv %>% 
  filter(between(end_lng, lng_min, lng_max) & 
          between(end_lat, lat_min, lat_max) &
          between(start_lng, lng_min, lng_max) &
          between(start_lat, lat_min, lat_max))

rm(lat_max, lat_min, lng_max, lng_min)

Result:

• Number of removed stations: 8
  
• Number of remaining rows : 4,367,845
  
  
  

2.2.4 Remove duplicate rows

In order to detect and remove duplicates we will compare all columns except the unique ride_id:

df_trips_all_clean_dup <- df_trips_all_clean_serv %>% 
  distinct(rideable_type,
           started_at,
           ended_at,
           start_station_name,
           start_station_id,
           end_station_name,
           end_station_id,
           start_lat,
           start_lng,
           end_lat,
           end_lng,
           member_casual,
           .keep_all = TRUE
  )
rm(df_trips_all_clean_serv)

Result:

• Number of duplicate rows removed: 22
  
• Number of remaining rows: 4,367,823
  
  
  

2.3 Handling dates

The imported data with time-stamps for start and end time are recorded in local time (“America/Chicago” Central Time). In order to account for daylight saving time (DST) the data and system environment of RStudio have to be set to the same local time-zone (TZ).

2.3.1 Setting the correct time-zone

The time-zone of the imported raw data are set by default to TZ = “UTC”. Since the time-stamps were recorded in local time we have to change the time zone of the data and the system environment.
Note: The local standard time-zone like (CST - Central Standard Time) does not have daylight saving times and using it will result in wrong ride-time calculations.

Set the system environment TZ:

Setting the system time to local time “America/Chicago”:

# Set environment time zone
Sys.setenv(TZ = "America/Chicago")

# confirm time-zone of system
Sys.timezone()

## [1] "America/Chicago"

Result: System time-zone set to “America/Chicago”

Set date TZ:

Forcing TZ “America/Chicago” on time-stamps:

df <- df_trips_all_clean_dup

## Force  time-zone "America/Chicago" on dates without changing the values:
df$started_at <- force_tz(df$started_at, tz = "America/Chicago")
df$ended_at <- force_tz(df$ended_at, tz = "America/Chicago")

## check TZ
attr(df$ended_at, "tzone")

## [1] "America/Chicago"

attr(df$started_at, "tzone")

## [1] "America/Chicago"

Result: Date time-zone set to “America/Chicago”

2.3.2 Correcting for Daylight Saving Time

Spring: Advancing clock - time gap

In spring on 2022-03-13 02:00:00 the time is advanced by 1 hour. There is no time recording for 02:00:00 - 02:59:59. I.e. 01:59:59 + 1 sec = 03:00:00. Ride-time calculation by simple subtraction will create an error of +60 min. The calculation will be automatically corrected by the function difftime()

Checking the correct calculation for rides during the time gap:

# Spring DST check
df_dst_spring <- df %>% 
  filter((started_at >  '2022-03-13 01:55:00' &
            started_at < '2022-03-13 03:01:00')) %>%   
  mutate(ride_time = difftime(ended_at, started_at, units = 'mins')) %>% 
  select(started_at, ended_at, ride_time) %>% 
  arrange(started_at)

print(df_dst_spring)

## # A tibble: 2 × 3
##   started_at          ended_at            ride_time    
##   <dttm>              <dttm>              <drtn>       
## 1 2022-03-13 01:57:29 2022-03-13 03:02:53 5.400000 mins
## 2 2022-03-13 01:57:57 2022-03-13 03:05:34 7.616667 mins

rm(df_dst_spring)

  Result: Calculation is correct. Time gap of 60 minutes skipped in calculation

Fall: Returning clock - time lap

In autumn on 2022-11-06 02:00:00 the time is returned by 1 hour. The time between 01:00:00 and 01:59:59 is recorded twice. To eliminate ambiguity, the time would have had to be measured in UTC (e.g. GPS tracker). In our data set however the time is measured in local time. Thus we cannot determine whether the time stamp belongs to the first path (before DST switch) or the second path (after DST switch). Therefore, we will remove all time stamps originated or ended between 1am to 2am. Rides originated before 1am and ended after 2am will be automatically corrected by the function difftime()

Number of dates time slot at DST lap:

df %>% 
  filter(
    (started_at >  '2022-11-06 01:00:00' &
     started_at < '2022-11-06 02:00:00') |
    
    (ended_at >  '2022-11-06 01:00:00' &
     ended_at < '2022-11-06 02:00:00')
    ) %>% 
  nrow()

## [1] 341

Result: 341 rows are affected

Removing dates from time slot at DST lap:

df_trips_all_clean_dst <- df %>% 
  filter(
    !((started_at >  '2022-11-06 01:00:00' &
       started_at < '2022-11-06 02:00:00') |
      
      (ended_at >  '2022-11-06 01:00:00' &
       ended_at < '2022-11-06 02:00:00'))
  )

Result:

• Number of rows removed: 341
  
• Number of rows remaining: 4,367,482
  
  
  

2.3.3 Remove rows with time dependency conflict: starttime > endtime

There are still some rides where the end time is before the start time.

df_trips_all_clean_dst %>% 
  filter(difftime(ended_at, started_at, units = 'mins') < 0) %>% 
  nrow()

## [1] 37

Result: There are 37 rides with negative ride time. All rides originated and ended at the same station

Remove rides with datetime dependency conflict:

df_trips_all_clean_time <- df_trips_all_clean_dst %>% 
  filter(!(difftime(ended_at, started_at, units = 'mins') < 0))

rm(df_trips_all_clean_dup, df_trips_all_clean_dst, df)

Result:

• Number of rows with time conflicts removed: 37
  
• Number of remaining rows: 4,367,445
  
  
  
  

2.4 Transform data

2.4.1 Add calculated variables for duration, weekdays, and hours

For further analysis we will now calculate the ride time (duration) and extract year, month_name, day_name and hour from start time.

# add columns for ride duration, year, month, day, weekday, hour
df_trips_all_trans <- df_trips_all_clean_time %>% 
  mutate(ride_time = as.numeric(difftime(ended_at, started_at, units = 'mins')),
         year = year(started_at),
         month_name = month(started_at, label = TRUE),
         weekday = wday(started_at, label = TRUE),
         hour = hour(started_at)
  )
rm(df_trips_all_clean_time)

2.4.2 Format categorical variables to factors

We will now convert categorical variables into factors with defined ordered levels. This will allow us to apply useful graphics:

df <- df_trips_all_trans

df$rideable_type <- factor(df$rideable_type, ordered = TRUE)
df$member_casual <- factor(df$member_casual, ordered = TRUE)
df$hour <- factor(df$hour, ordered = TRUE)

# clean up
df_trips_all_fct <- df
rm(df, df_trips_all_trans)

2.4.3 Add sub-groups for time categories:

We will now add sub-groups for season, week and day defined as follows:

• season: winter, spring, summer, autumn
  
• day_type: weekend, workday
  
• hour_type: night, morning, afternoon, evening
  

df_trips_all_fct <- df_trips_all_fct %>% 
  mutate(season = fct_collapse(month_name, 
                      winter = c("Jan", "Feb", "Mar"),
                      spring = c("Apr", "May", "Jun"),
                      summer = c("Jul", "Aug", "Sep"),
                      autumn = c("Oct", "Nov", "Dec")
                      ),
         day_type = fct_collapse(weekday,
                      workday = c("Mon", "Tue", "Wed", "Thu", "Fri"),
                      weekend = c("Sat", "Sun")
                      ),
         hour_type = fct_collapse(hour,
                      night = c("0", "1", "2", "3", "4", "5"),
                      morning  = c("6", "7", "8", "9", "10", "11"),
                      afternoon = c("12", "13", "14", "15", "16", "17"),
                      evening = c("18", "19", "20", "21", "22", "23")
                      )
         )

2.5 Treatment of outliers

2.5.1 Identify outliers

First let’s explore the distribution of ride_time by user group and bike type to identify possible outliers.

df_trips_all_fct %>% 
  group_by(member_casual, rideable_type) %>% 
  summarise(Total_num_of_rides = n(),
            min_ride_time = min(ride_time),
            max_ride_time = max(ride_time))

## # A tibble: 5 × 5
## # Groups:   member_casual [2]
##   member_casual rideable_type Total_num_of_rides min_ride_time max_ride_time
##   <ord>         <ord>                      <int>         <dbl>         <dbl>
## 1 casual        classic_bike              888659             0         1499.
## 2 casual        docked_bike               174811             0        32035.
## 3 casual        electric_bike             693784             0          480.
## 4 member        classic_bike             1708456             0         1493.
## 5 member        electric_bike             901735             0          480

Result:

• max ride time classic bikes is 1499 min (about 24 hours)
  
• max ride time of electric bikes is 480 min (8 hours)
  
• max ride time of docked bikes is 32,000 min (about 22 days)
  
• min ride time is zero for all groups
  

To get more insight into the data we will use histograms for each group:

df_trips_all_fct %>% 
  ggplot() +
  geom_histogram(aes(ride_time), binwidth = 100) +
  coord_cartesian(ylim = c(0,10)) +
  scale_x_continuous(labels = scales::label_number_si(),
                     breaks = seq(0, 35000, by = 10000)) +
  scale_y_continuous(breaks = seq(0, 10, by = 2)) +
  xlab("Ride time (min)") +
  ylab("Rides")+
  labs(title = "Histogram zoomed-out")+
  facet_grid(member_casual~rideable_type)+
   theme(plot.title.position = "plot",
          axis.title.y = element_text(hjust = 1),
          axis.title.x = element_text(hjust = 0)
        )

Result: apparently only the docked_bike type shows outliers. Let’s zoom-in to ride time 1,500 minutes:

df_trips_all_fct %>% 
  ggplot() +
  geom_histogram(aes(ride_time), binwidth = 10) +
  coord_cartesian(ylim = c(0,10),
                  xlim = c(0,2000)) +
  scale_x_continuous(labels = scales::label_number_si(),
                     breaks = seq(0, 2000, by = 500)) +
  scale_y_continuous(breaks = seq(0, 10, by = 2)) +
  xlab("Ride time (min)") +
  ylab("Rides")+
  labs(title = "Histogram zoomed-in")+
  facet_grid(member_casual~rideable_type)+
   theme(plot.title.position = "plot",
          axis.title.y = element_text(hjust = 1),
          axis.title.x = element_text(hjust = 0)
        )

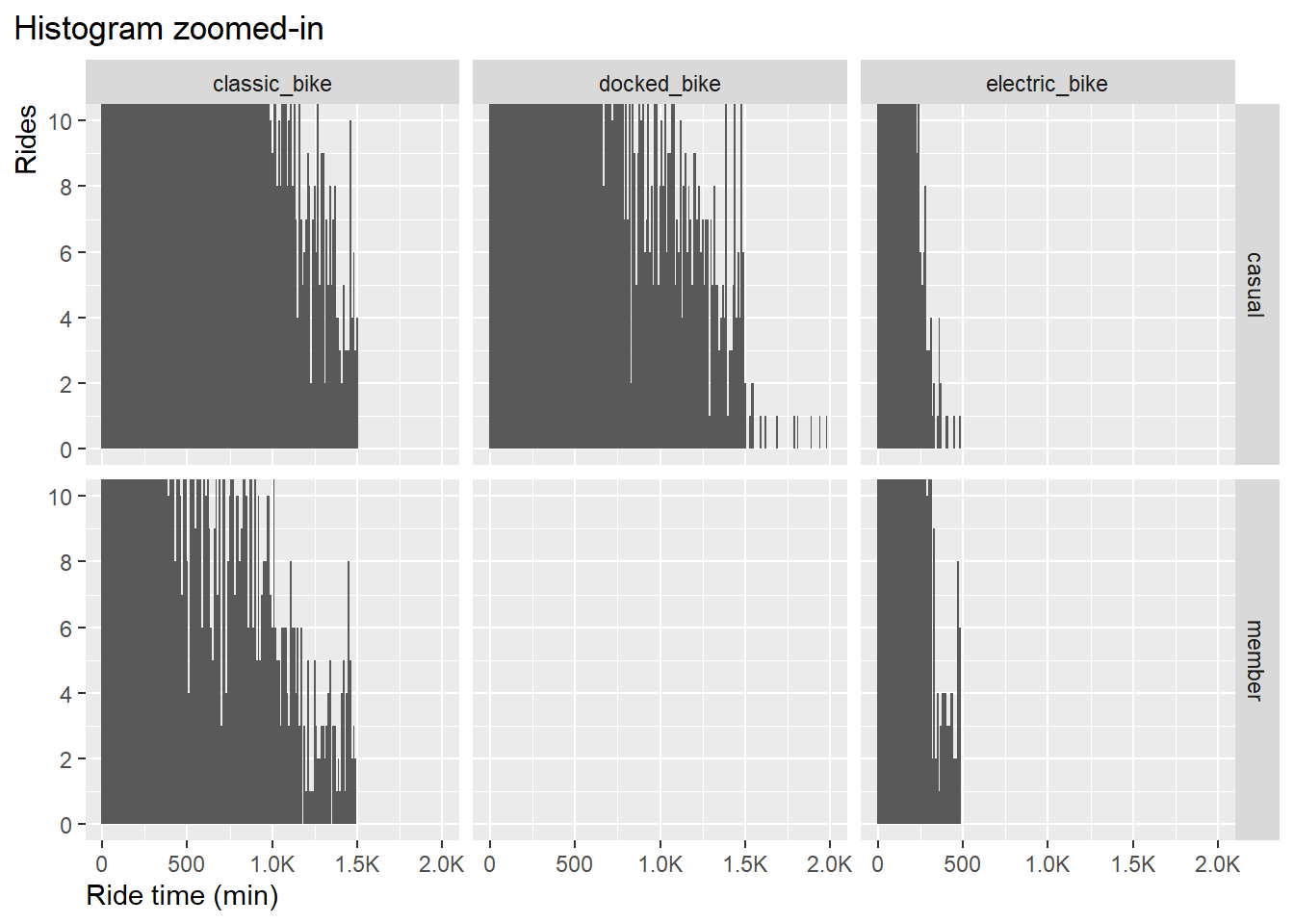
Result:

• ride time with classic bikes is capped at around 1500 min in both user groups.
  
• ride time with electric bikes is capped at around 500 min in both user groups.
  
• ride time with docked bikes has values beyond 1500 min.
  

We don’t see evidence for outliers in groups classic bike and electric bike due to its continuous distribution, However, in the case of docked bikes we see an sudden change in the pattern, a kind of noise starting from 1500.
Therefore, the upper threshold to remove outlier will be set to 1500 minutes.

We make the decision to set the lower threshold to 1 minute. Rides less than 1 minute can be classified as bike management to dock and release bikes in order to reset the rent status. For more details see DIVVY pricing program in page “Introduction/Appendix”.

2.5.2. Remove outliers

Now, after we have defined the boundary values [1, 1500] let’s remove the outliers:

low <- 1
up <- 1500

df_trips_all_final <- df_trips_all_fct %>% 
  filter(!(ride_time < low | ride_time > up))

rm(df_trips_all_fct, low, up)

Result:

• Removed outliers: 76,473
  
• Remaining rows: 4,290,971
  
  
  

2.6 Export cleaned data frame

2.6.1 Remove irrelevant variables

The following variables will be removed from the dataframe, as they are not essential for the further analysis

• ride_id
  
• ended_at
  
• start_station_id
  
• end_station_id
  
• year

df_trips_all_final_dense <- df_trips_all_final %>% 
  select(bike_type = rideable_type,
         start_time = started_at,
         start_station = start_station_name,
         end_station = end_station_name,
         start_latitude = start_lat,
         start_longitude = start_lng,
         end_latitude = end_lat,
         end_longitude = end_lng,
         user = member_casual,
         ride_time,
         month_name,
         weekday,
         hour,
         season,
         day_type,
         hour_type
         )
rm(df_trips_all_final)

2.6.2 Export cleaned file

NOTE: ordered factor setting will be lost in the CSV file. Therefore, we will create an RDS file that can be used to in the rMarkdown file for analysis.

V. Data Analysis in R

Pre-requisites

Global settings for scale and color:

### switch scientific number output OFF with "option(scipen = 999)" and ON with "option(scipen = 0)"
options(scipen = 999)

### set color table (global)
color_table <- tibble(
  users = c("casual", "member"),
  color = c("darkgreen", "blue"))

For better readability we will rename the long dataframe name into a short name:

df <- df_trips_all_final_dense
# str(df)
# summary(df)
rm(df_trips_all_final_dense)

Dataframe names:

• df: dataframe with cleaned data
• df_corr: dataframe for correlation analysis
• color_table: dataframe with color definition

3. Data analysis and visualization

3.1 Descriptive statistics

3.1.1 Distribution of ride-time in a histogram graph

Let’s first get an overview of the ride-time distribution in each group by histograms:

df %>% 
  ggplot() +
  geom_histogram(aes(x = ride_time, fill = user, color = "lightblue"), binwidth = 2)+
  scale_fill_manual(values = color_table$color)+
  xlab("ride-time") +
  ylab("Rides")+
  coord_cartesian(xlim = c(0,120)) +
  scale_y_continuous(labels = scales::label_number_si(),
                     breaks = seq(0, 400000, by = 100000))+
  labs(title = "Distribution of ride-time",
       subtitle = "Jan-Dec 2022") +
  facet_wrap(~user)+
  theme(legend.position = "none",
          plot.title.position = "plot",
          axis.title.y = element_text(hjust = 1),
          axis.title.x = element_text(hjust = 0)
        )

Result:

• The shapes of both distributions are similar, skewed to the right (long tail)
  
• The distribution of casuals is slightly wider than that of members
  
  

3.1.2 Key measures as table

Next let’s calculate for each user group the totals, mean, standard deviation and other statistical measures:

# ----------------------------------------------------------------------- totals
# Calculate totals
sum_ride_time <- sum(df$ride_time)
n_all <-length(df$ride_time)

# ------------------------------------------------ Aggregate KPIs for user group
df1 <- df %>% 
  group_by(user) %>% 
  summarise(rides = round(n()/1000,2), 
            prop_rides = round(n()/n_all*100,0),
            total_ride_time = round(sum(ride_time)/1000000,2), 
            prop_total_ride_time = round(sum(ride_time)/sum_ride_time*100,0),
            avg_ride_time = round(mean(ride_time),1),
            sd_ride_time = round(sd(ride_time), 1),
            med_ride_time = round(median(ride_time),1),
            quantile_lower = round(quantile(ride_time, 0.25),1),
            quantile_upper = round(quantile(ride_time, 0.75),1),
            iqr = round(IQR(ride_time),1)
            )


# ------------------------------------- Pivot dataframe for better visualization
df2 <- df1 %>% 
  pivot_longer(c(`rides`,
                 `prop_rides`,
                 `total_ride_time`,
                 `prop_total_ride_time`,
                 `avg_ride_time`,
                 `sd_ride_time`, 
                 `med_ride_time`, 
                 `quantile_lower`,
                 `quantile_upper`,
                 `iqr`),
               names_to = "Statistical values (Jan-Dec, 2022)", values_to = "values")

df3 <- df2 %>% 
  pivot_wider(names_from = user, values_from = values)

# ----------------------------------------------------- rename stat measures
df4 <- df3
df4[df4 == "rides"] <- "Total rides [Tausend]"
df4[df4 == "prop_rides"] <- "Proportion total rides [%]"
df4[df4 == "total_ride_time"] <- "Total ride-time [Million min]"
df4[df4 == "prop_total_ride_time"] <- "Proportion total ride-time [%]"
df4[df4 == "avg_ride_time"] <- "Avg. ride-time [min]"
df4[df4 == "sd_ride_time"] <- "Standart deviation ride-time [min]"
df4[df4 == "med_ride_time"] <- "Median ride-time [min]"
df4[df4 == "quantile_lower"] <- "Quantile lower [min]"
df4[df4 == "quantile_upper"] <- "Quantile upper [min]"
df4[df4 == "iqr"] <- "Inter quartile range IQR [min]"


df_kpis <- df4    #------------------------------------------------- set df name

# --------------------------------------------------------------- print as table
knitr::kable(df_kpis[1:10 , ])

Statistical values (Jan-Dec, 2022)	casual	member
Total rides [Tausend]	1730.37	2560.60
Proportion total rides [%]	40.00	60.00
Total ride-time [Million min]	41.74	32.48
Proportion total ride-time [%]	56.00	44.00
Avg. ride-time [min]	24.10	12.70
Standart deviation ride-time [min]	43.20	19.10
Median ride-time [min]	14.10	9.20
Quantile lower [min]	8.10	5.40
Quantile upper [min]	26.10	15.60
Inter quartile range IQR [min]	18.00	10.10

# --------------------------------------------------------------------- clean up
rm(df1, df2, df3, df_kpis, n_all, sum_ride_time)

3.1.3 Key measures as bar graphs

Graph: Total number of rides, total ride-time and average ride-time by user group. In a skewed distribution the average-value (mean) is not so meaningful, instead we will use the median-value:

# ---------------------------------------------------- bar graph for total rides
pl1 <- df %>% 
  group_by(user) %>% 
    summarise(n = n()) %>%
    mutate(frq_n = n/sum(n)) %>% 
  
  ggplot(aes(x = user, y = n))+
    geom_bar(stat = "identity", aes(fill = user))+
    scale_fill_manual(values = color_table$color)+
    labs(title = "Total number of rides") +
    coord_cartesian(ylim = c(0,3000000)) +
    xlab("") +
    ylab("Rides [Million]") +
    scale_y_continuous(labels = scales::label_number_si())+  
    geom_text(aes(y = n, label = paste0('(', scales::percent(frq_n), ')')), vjust=-0.5, size=3)+
    theme(legend.position = "none",
          plot.title.position = "plot",
          axis.title.y = element_text(hjust = 1))

# ------------------------------------------------ bar graph for total ride-time
pl2 <- df %>% 
  group_by(user) %>% 
  summarise(rt = as.double(sum(ride_time))) %>%
  mutate(frq_rt = rt/sum(rt)) %>% 
  
  ggplot(aes(x = user, y = rt))+
  geom_bar(stat = "identity", aes(fill = user))+
  scale_fill_manual(values = color_table$color)+
  labs(title = "Total ride-time") +
  coord_cartesian(ylim = c(0,50000000)) +
  xlab("") +
  ylab("ride-time [Million min]") +
  scale_y_continuous(labels = scales::label_number_si())+
  geom_text(aes(y = rt, label = paste0('(', scales::percent(frq_rt), ')')), vjust=-0.5, size=3)+
 theme(legend.position = "none",
          plot.title.position = "plot",
          axis.title.y = element_text(hjust = 1))

# ---------------------------------------------- bar graph for median ride-time
pl3 <- df %>% 
  group_by(user) %>% 
  summarise(med_rt = round(median(ride_time),1)) %>%
  
  ggplot(aes(x = user, y = med_rt))+
  geom_bar(stat = "identity", aes(fill = user))+
  scale_fill_manual(values = color_table$color)+
  labs(title = "Median ride-time") +
  coord_cartesian(ylim = c(0,25)) +
  xlab("") +
  ylab("Median ride-time [min]") +
  geom_text(aes(y = med_rt, label = paste0(med_rt)), vjust = -0.5, size = 3)+
  theme(legend.position = "none",
          plot.title.position = "plot",
          axis.title.y = element_text(hjust = 1))

# --------------------------------------------------- display plots in one graph
# install and load package "gridExtra"
grid.arrange(pl1, pl2, pl3, ncol = 3)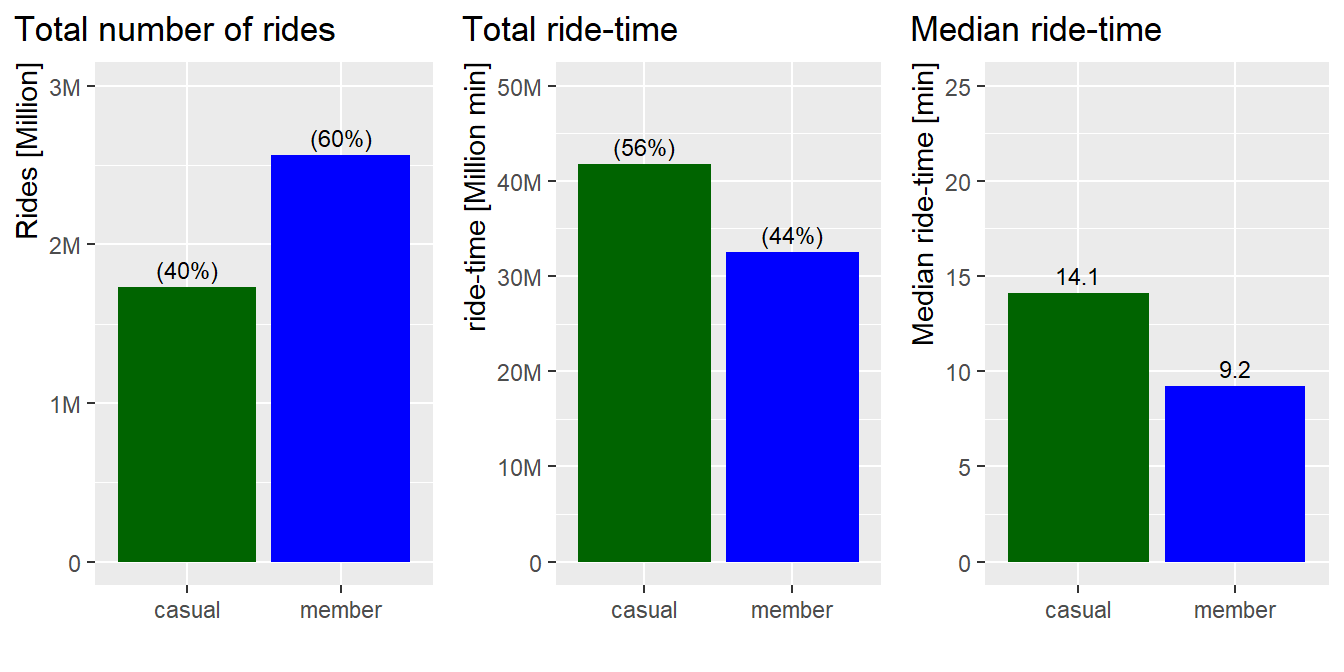

rm(pl1, pl2, pl3)

Result:

• Members have more rides per year than casuals
  
• Casuals have longer total ride-time
  
• Casuals’ median ride-time is about 5 minutes longer that that of members’ ride-time
  
  
  

3.1.4 Key measures by boxplot

For better understanding of the ride-time distribution we will use a boxplot:

data_means <- df %>% 
  group_by(user)%>%
  summarise(mean = mean(ride_time))

df %>% 
  ggplot(aes(x = user, y = ride_time, color = user))+
  stat_boxplot(geom = "errorbar") +
  geom_boxplot()+
  stat_summary(fun = mean, geom = "point", size = 5) +
  scale_color_manual(values = color_table$color)+
  labs(title = "Distribution of ride-time") +
  xlab("") +
  ylab("ride-time (min)") +
  coord_cartesian(ylim = c(0,60)) +

# ------------------------------------------------------ annotation for casuals    
  annotate("text", x=0.57, y=8, label="25%", size = 3)+
  annotate("text", x=0.57, y=15, label="50%", size = 3)+
  annotate("text", x=0.57, y=27, label="75%", size = 3)+
  annotate("text", x=1.44, y=8, label=as.numeric(df4[8,2]), size=3)+    # q1
  annotate("text", x=1.44, y=27, label=as.numeric(df4[9,2]), size=3)+   # q3
  annotate("text", x=0.9, y=16, label="median", size = 3)+            
  annotate("text", x=1.1, y=16, label=as.numeric(df4[7,2]), size=3)+    # median
  annotate("text", x=0.9, y=24.4, label="mean", size = 3)+
  annotate("text", x=1.1, y=24.4, label=as.numeric(df4[5,2]), size=3)+  # mean  
  
# ------------------------------------------------------ annotation for members     
  
  annotate("text", x=2.44, y=5.3, label=as.numeric(df4[8,3]), size=3)+  # q1
  annotate("text", x=2.44, y=9.2, label=as.numeric(df4[7,3]), size=3)+  # median
  annotate("text", x=2.44, y=15.5, label=as.numeric(df4[9,3]), size=3)+ # q3
  annotate("text", x=2.1, y=12.7, label=as.numeric(df4[5,3]), size=3)+  # mean
  
  theme(legend.position = "none",
          plot.title.position = "plot",
          axis.title.y = element_text(hjust = 1),
          axis.title.x = element_text(hjust = 0)
        ) 

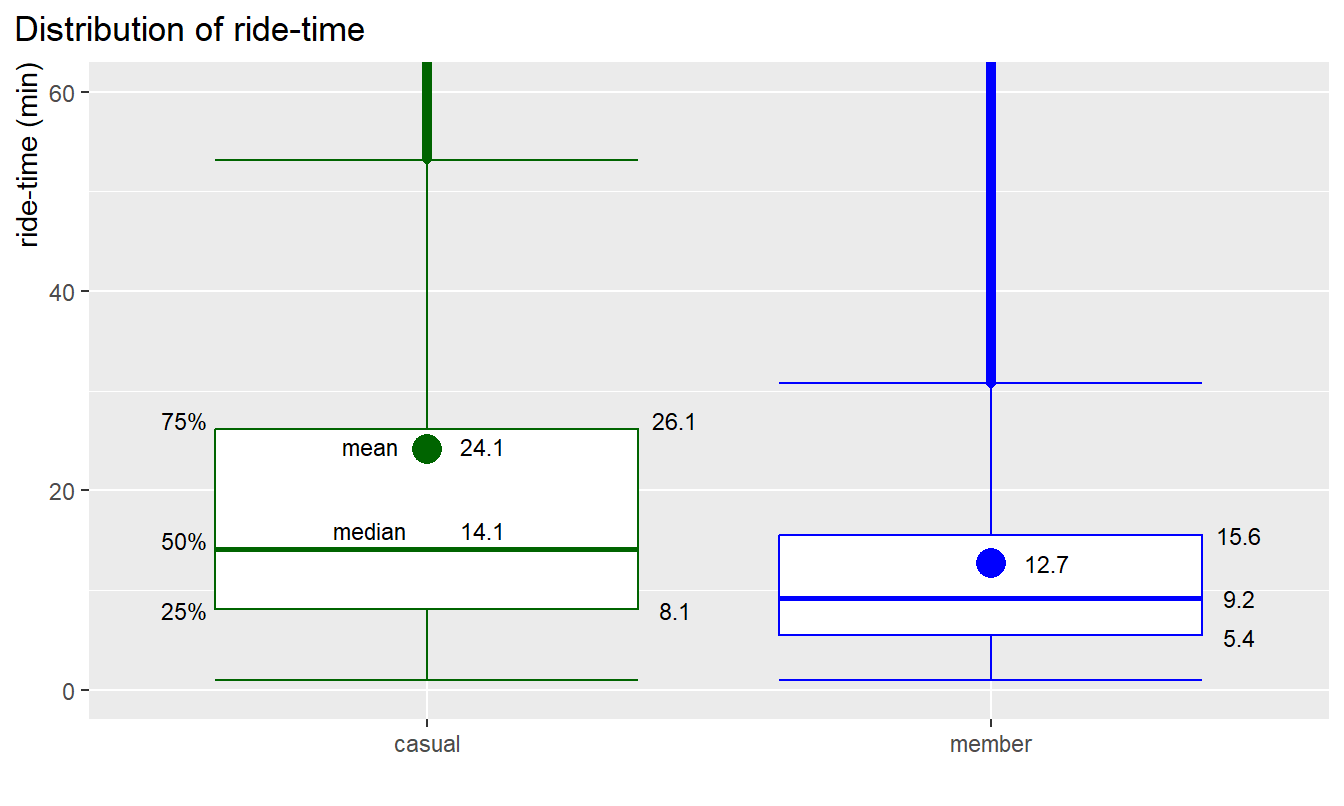
rm(data_means, df4)

  How to read the boxplot:

• The middle line marks the mid-point at 50% or median (middle quartile)
  
• The lower box line (lower quartile) marks 25% of all values, the upper box line (upper quartile) marks 75% of all values, the box height contains, therefore, 50% of all values (ride-time),
• The extended vertical lines (whiskers) represent more extreme values. The longer these lines are the higher the spread is
  
• Every values below or above the whiskers are potential outliers
  
• The big dot mark in the box is the mean value. For ideal normal distribution the median and the mean should be the same or very close
  
  

Results for casuals:

• 75% of rides by casuals are shorter than 26 min
  
• 50% of values (IQR) are between 8 to 26 min
  
• The median point (mid-point) is at 14 min
  
• The mean point is at 24 min
• The spread is wide and even more skewed because mean and median are far apart
  
  

Results for members:

• 75% of rides by members are shorter than 16 min
  
• 50% of values (IQR) are between 5 to 16 min
  
• The median point (mid-point) is at 9 min
  
• The mean point is at 13 min
  
• The spread is more contained around the median and mean, i.e annual members typical ride-time is quite constant
  
  

3.1.5. Log transform ride-time data for normalization

Since the data are highly skewed a statistical test, like t-test, is not meaningful. The data can however be normalized using a log transformation.

Preparing a dataset with log-trans values:

df_log <- df %>% 
  filter(!is.na(ride_time)) %>% 
  mutate(ride_time_log = log10(ride_time)) %>% 
  select(user, ride_time_log)

Histogram of log-trans values:

df_log %>% 
  ggplot() +
  geom_histogram(aes(x = ride_time_log, fill = user, color = "lightblue"), binwidth = 0.1)+
  scale_fill_manual(values = color_table$color)+
  xlab("log10(ride-time)") +
  ylab("Rides")+
  coord_cartesian(xlim = c(-2,4)) +
  scale_y_continuous(labels = scales::label_number_si(),
                     breaks = seq(0, 400000, by = 100000))+
  labs(title = "Distribution of log10(ride-time)",
       subtitle = "Jan-Dec 2022") +
  facet_wrap(~user)+
  theme(legend.position = "none",
          plot.title.position = "plot",
          axis.title.y = element_text(hjust = 1),
          axis.title.x = element_text(hjust = 0)
        )

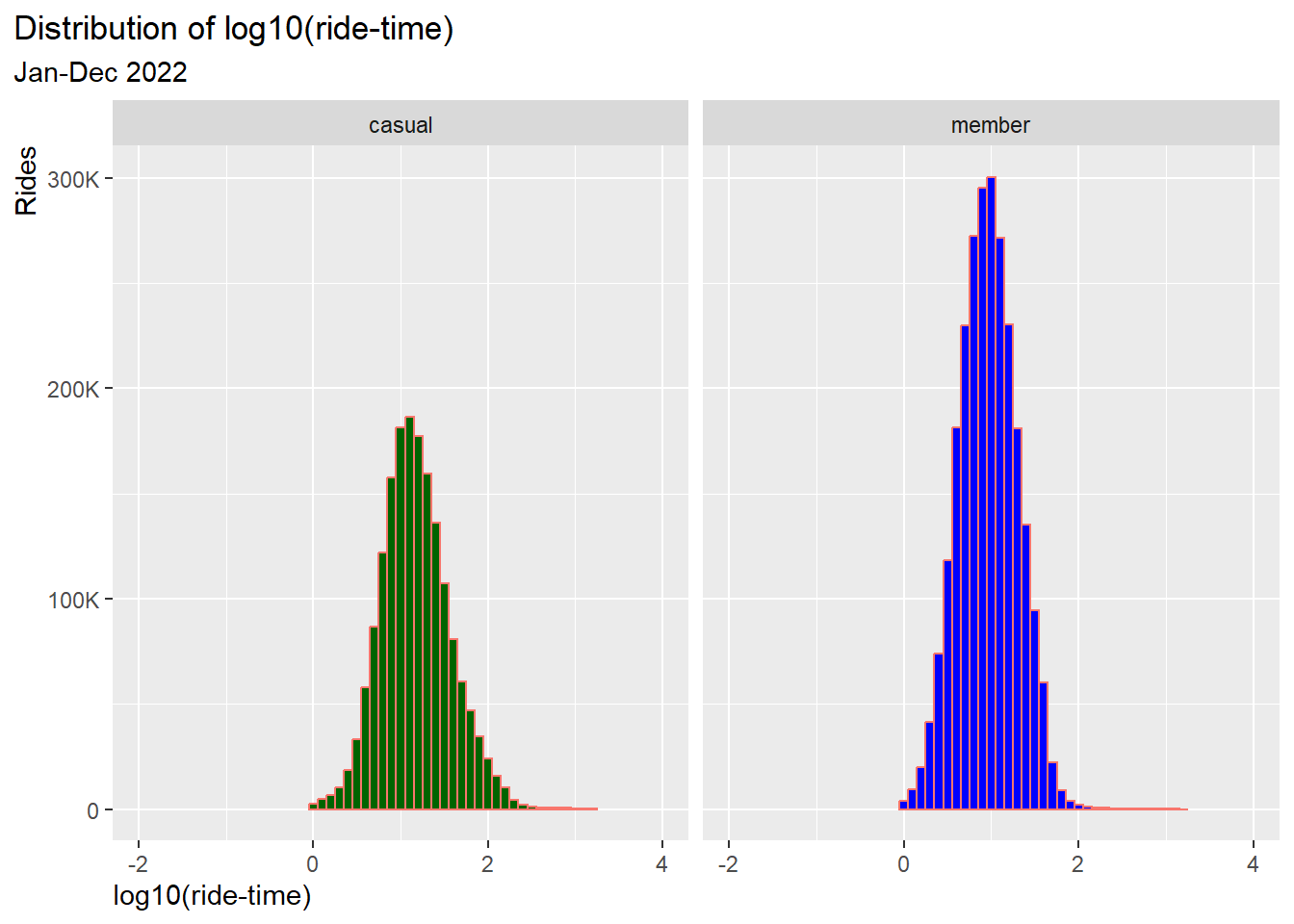
Result: the distribution is now normalized

Boxplot of log-trans values:

data_means <- df_log %>% 
  group_by(user)%>%
  summarise(mean = mean(ride_time_log))

df_log %>% 
  ggplot(aes(x = user, y = ride_time_log, color = user))+
  stat_boxplot(geom = "errorbar") +
  geom_boxplot()+
  stat_summary(fun = mean, geom = "point", size = 5) +
  scale_color_manual(values = color_table$color)+
  labs(title = "Distribution of log10(ride-time)") +
  xlab("") +
  ylab("log10(ride-time)") +
  coord_cartesian(ylim = c(0,3.5)) +

  
  theme(legend.position = "none",
          plot.title.position = "plot",
          axis.title.y = element_text(hjust = 1),
          axis.title.x = element_text(hjust = 0)
        ) 

rm(data_means)

Result: The boxplots are now symmetric, i.e. normalized, mean and median are almost identical.

T-test to test if the difference in mean between groups is statistically significant:

• Ho-hypothesis: there is no significant difference between both means
  
• Ha-hypothesis (alternative): there is a significant difference between both means
  

tt <- t.test(ride_time_log ~ user, data = df_log)

names <- c("p-value", "geometric mean casuals", "geometric mean members")
values <- c(
  tt$p.value,
  round((10 ** tt$estimate[[1]]),1),
  round((10 ** tt$estimate[[2]]),1)
)
tt_values <- data.frame(names, values)
print(tt_values)

##                    names values
## 1                p-value    0.0
## 2 geometric mean casuals   15.0
## 3 geometric mean members    9.2

rm(tt, names, values, tt_values, df_log)

Result:

• The mean values calculated through the log10 transformation are very close to the median and their difference is statistical significant with p-value = 0
  
• geometric mean casual = 15.0
  
• geometric mean member = 9.2
  
  

3.1.5 Conclusion: Descriptive statistical values

• The distribution of ride-time in both groups is skewed to the right, i.e. concentration of shorter rides and fewer longer rides
  
• Annual members ride more than casual riders over the year
  
• Annual riders accumulate more ride-time over the year than annual members
  
• The median ride-time (equivalent to geom. mean) of casual riders is significantly higher than for annual members
  
• The ride-time of casual riders shows more fluctuations, whereas the ride time of members is more contained around the mid-point
  
  
  

3.2 Time dependencies

3.2.1 Number of rides as time series

Let’s first get an overview of the whole year cycle by number of rides aggregated by day:

# ------------------------------------------- binwidth = 24 hours (3600*24 sec)
df %>% 
  ggplot(aes(x = start_time, color = user)) +
  geom_freqpoly(binwidth = 3600*24, linewidth = 1)+
  scale_color_manual(values = color_table$color)+
  labs(title = "Total number of rides over time",
       subtitle = "Daily aggregates 2022") +
  xlab("") +
  ylab("Rides")+
  scale_y_continuous(labels = scales::label_number_si(),
                     breaks = seq(0, 25000, by = 5000))+
  facet_wrap(~user, nrow = 2) +
  theme(plot.title.position = "plot",
          axis.title.y = element_text(hjust = 1),
          axis.title.x = element_text(hjust = 0)
        )

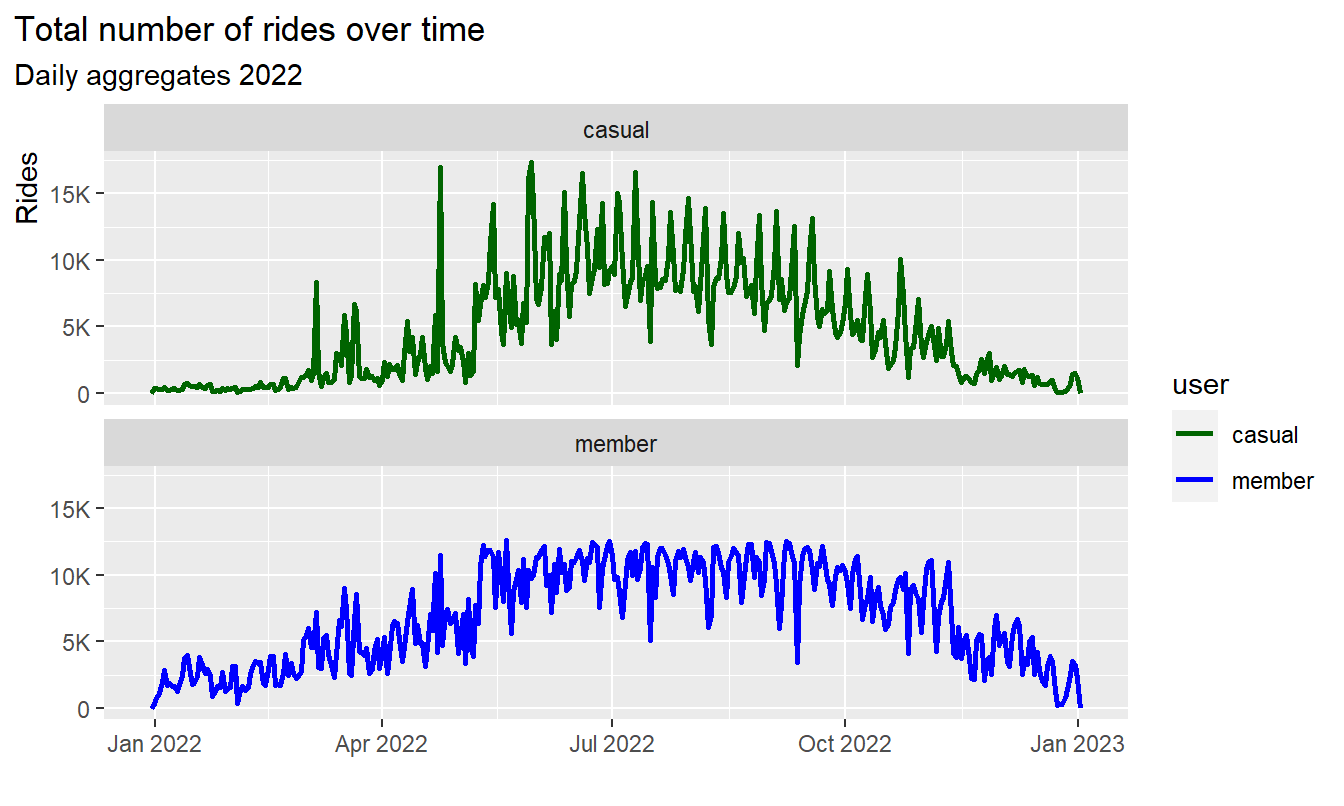
Result:

• Both signals show multiple overlapping cycles of different frequencies over year, week and day
  
• There are similarities but also differences
  

Let’s brake down the signal by month, day and hour:

3.2.2 Annual cycle by month

We will plot the number of rides over year aggregated by months in absolute values and in relative values
Relative frequency is calculated by : frq_rides = n_month/n_year per group:

# ------------------------------------------------- line chart number of rides
pl1 <- df %>% 
  group_by(user, month_name) %>% 
  summarise(n = n()) %>%

  ggplot(aes(x = month_name, y = n, group = user, color = user)) +
  geom_line(size = 1.5, alpha = 0.5) +
  geom_point(size = 2) +
  scale_color_manual(values = color_table$color) +
  labs(title = "Number of rides by month in 2022",
       subtitle = "Absolut values, monthly aggregates") +
  coord_cartesian(ylim = c(0,400000)) +
  xlab("") +
  ylab("Rides [Thausend]") +
  scale_y_continuous(labels = scales::label_number_si())+
  scale_x_discrete(labels = abbreviate) +
  theme(legend.position = c(0.93, 0.83),
        legend.title = element_blank(),
        legend.text = element_text(size=8),
        legend.background = element_blank(),
          plot.title.position = "plot",
          axis.title.y = element_text(hjust = 1)
        )
  
# ----------------------------------------------- line chart frequency of rides
pl2 <- df %>% 
  group_by(user, month_name) %>% 
  summarise(n = n()) %>%
  mutate(frq_n = n/sum(n)) %>% 
  
  ggplot(aes(x = month_name, y = frq_n, group = user, color = user)) +
  geom_line(size = 1.5, alpha = 0.5) +
  geom_point(size = 2) +
  scale_color_manual(values = color_table$color) +
  labs(title = "",
       subtitle = "Relative frequency",
       caption = "Rel. frequency = n_month / n_year") +
  coord_cartesian(ylim = c(0,0.2)) +
  xlab("") +
  ylab("Rel. frequency") +
  scale_y_continuous(labels = scales::label_number_si())+
  theme(legend.position = "none",
          plot.title.position = "plot",
          axis.title.y = element_text(hjust = 1)
        )
# ---------------------------------------------------------- display both plots 
# install and load package "gridExtra"
grid.arrange(pl1, pl2, nrow = 2)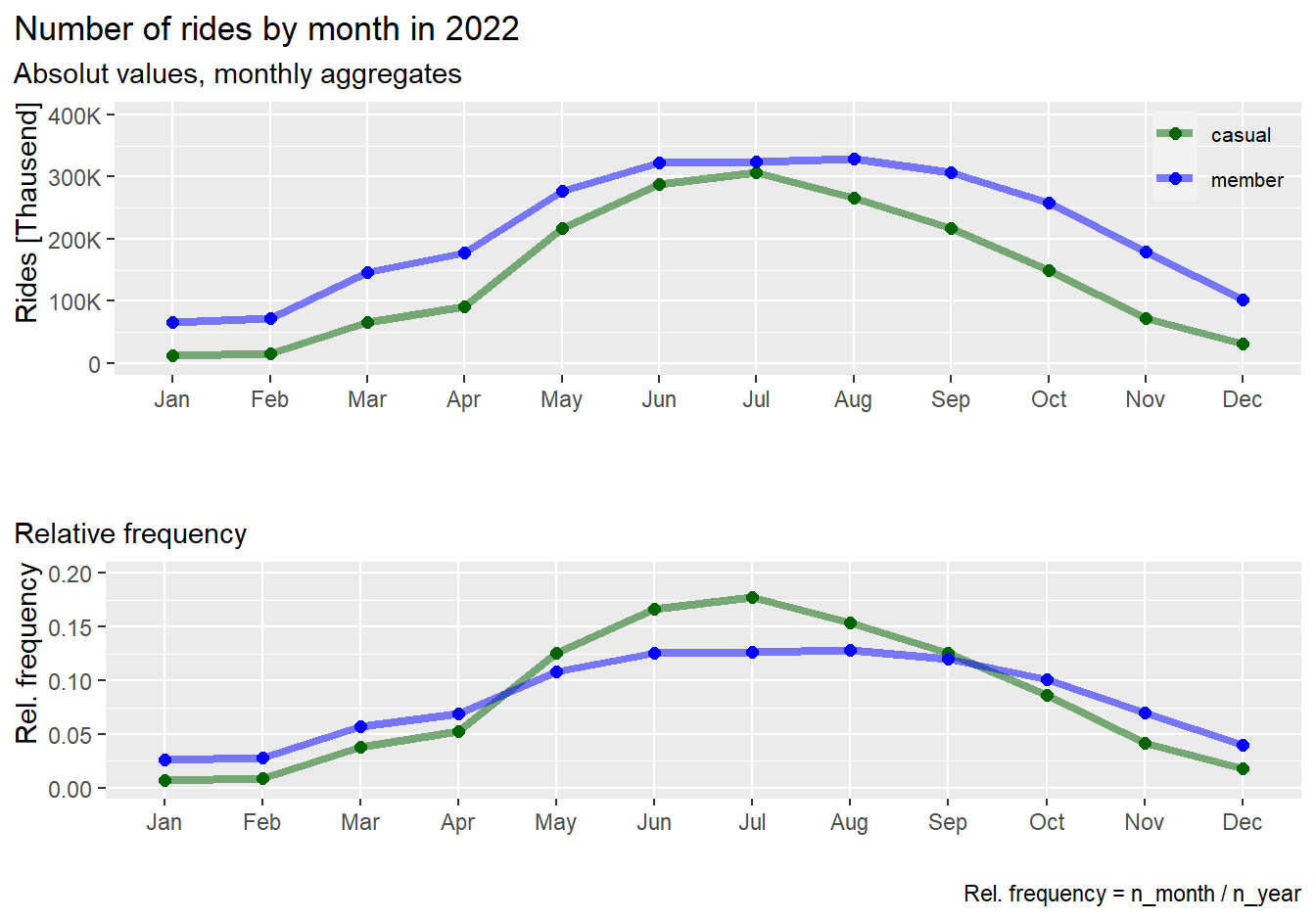

rm(pl1, pl2)

Results:

• Both, casuals and members, show similar behavior over the year: Increase of rides in warmer months and decrease in colder months
  
• The number of rides by casuals is almost dropping down to zero in winter months January and February
  
• Relatively, casuals show a steeper increase of rides in warmer months compared to members
  
  

Average ride-time by month:

# ---------------------------------------------------- line chart avg. ride-time
df %>% 
  group_by(user, month_name) %>% 
  summarise(avg_rt = round(mean(ride_time),1)) %>%
  
  ggplot(aes(x = month_name, y = avg_rt, group = user, color = user)) +
  geom_line(size = 1.5, alpha = 0.5) +
  geom_point(size = 2) +
  scale_color_manual(values = color_table$color) +
  labs(title = "Average ride-time by month 2022",
       subtitle = "Monthly aggregates") +
  coord_cartesian(ylim = c(0,30)) +
  xlab("") +
  ylab("Avg. ride-time (min)") +
  scale_y_continuous(labels = scales::label_number_si())+
  theme(legend.position = c(0.93, 0.83),
        legend.title = element_blank(),
        legend.text = element_text(size=8),
        legend.background = element_blank(),
        plot.title.position = "plot",
        axis.title.y = element_text(hjust = 1)
        )

Results:

• The average ride-time of casuals is longer compared to members throughout the year
  
• The average ride-time of members is almost constant over the year, i.e. less dependent on seasons
  
• The average ride-time of casuals is longer in the warmer months, with peaks in March and May
  
  
  

3.2.3 Weekly cycle by day

Now, let’s plot the number of rides over a weak aggregated by days in absolute values and in relative values
Relative frequency is calculated by : frq_rides = n_day/n_year per group:

# ------------------------------------------------- line chart number of rides
pl1 <- df %>% 
  group_by(user, weekday) %>% 
  summarise(n = n()) %>%
  
  ggplot(aes(x = weekday, y = n, group = user, color = user)) +
  geom_line(size = 1.5, alpha = 0.5) +
  geom_point(size = 2) +
  scale_color_manual(values = color_table$color) +

  labs(title = "Number of rides by day in 2022",
       subtitle = "Absolut values, daily aggregates") +
  
  coord_cartesian(ylim = c(0,500000)) +
  xlab("") +
  ylab("Rides [Thausend]") +
  scale_y_continuous(labels = scales::label_number_si())+
  theme(legend.position = c(0.93, 0.23),
        legend.title = element_blank(),
        legend.text = element_text(size=8),
        legend.background = element_blank(),
          plot.title.position = "plot",
          axis.title.y = element_text(hjust = 1)
        )
# ----------------------------------------------- line chart frequency of rides
pl2 <- df %>% 
  group_by(user, weekday) %>% 
  summarise(n = n()) %>%
  mutate(frq_n = n/sum(n)) %>% 
  
  ggplot(aes(x = weekday, y = frq_n, group = user, color = user)) +
  geom_line(size = 1.5, alpha = 0.5) +
  geom_point(size = 2) +
  scale_color_manual(values = color_table$color) +
  
  labs(title = "",
       subtitle = "Relative frequency",
       caption = "Rel. frequency = n_day / n_year") +
  
  coord_cartesian(ylim = c(0.05,0.3)) +
  xlab("") +
  ylab("Rel. frequency") +
  scale_y_continuous(labels = scales::label_number_si())+
  theme(legend.position = "none",
          plot.title.position = "plot",
          axis.title.y = element_text(hjust = 1)
        )
# ---------------------------------------------------------- display both plots 
# install and load package "gridExtra"
grid.arrange(pl1, pl2, nrow = 2)

rm(pl1, pl2)

Results:

• Casuals and members, show opposite behavior over the week
  
• Members ride more on workdays, Monday to Friday, and less on weekends
  
• Casuals ride more on weekends and less on workdays
  
• The rides of casuals increases sharply on weekends
  
  

Average ride-time by day:

# ---------------------------------------------------- line chart avg. ride-time
df %>% 
  group_by(user, weekday) %>% 
  summarise(avg_rt = round(mean(ride_time),1)) %>%

  ggplot(aes(x = weekday, y = avg_rt, group = user, color = user)) +
  geom_line(size = 1.5, alpha = 0.5) +
  geom_point(size = 2) +
  scale_color_manual(values = color_table$color) +
  labs(title = "Average ride-time by day 2022",
       subtitle = "Daily aggregates") +
  coord_cartesian(ylim = c(0,30)) +
  xlab("") +
  ylab("Avg. ride-time") +
  scale_y_continuous(labels = scales::label_number_si())+
  theme(legend.position = c(0.93, 0.23),
        legend.title = element_blank(),
        legend.text = element_text(size=8),
        legend.background = element_blank(),
          plot.title.position = "plot",
          axis.title.y = element_text(hjust = 1)
        )

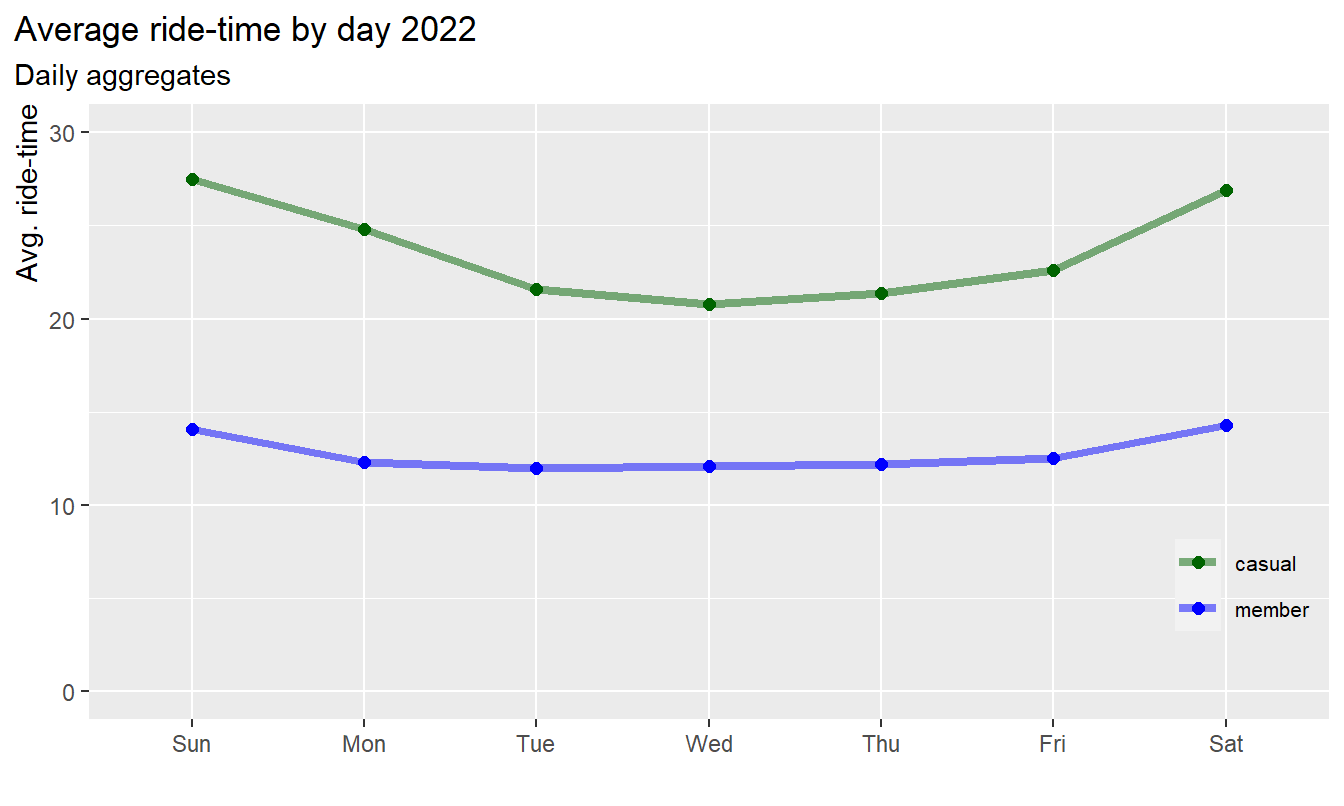
Results:

• The average ride-time of casuals is longer compared to members at all time
  
• The average ride-time of members is almost constant over the week, with slight increase on weekends
  
• The average ride-time of casuals is lowest on Wednesday and highest on Sunday, i.e. casuals ride longer from Friday to Monday
  
  
  

3.2.4 Daily cycle by hour

Finally, let’s plot the number of rides over a day aggregated by hours in absolute values and in relative values
Relative frequency is calculated by : frq_rides = n_hour/n_year per group:

# ------------------------------------------------- line chart number of rides
pl1 <- df %>% 
  group_by(user, hour) %>% 
  summarise(n = n()) %>%

  ggplot(aes(x = hour, y = n, group = user, color = user)) +
  geom_line(size = 1.5, alpha = 0.5) +
  geom_point(size = 2) +
  scale_color_manual(values = color_table$color) +
  
  labs(title = "Number of rides by hour in 2022",
       subtitle = "Absolut values, hourly aggregates") +
  
  coord_cartesian(ylim = c(0,300000)) +
  xlab("") +
  ylab("Rides") +
  scale_y_continuous(labels = scales::label_number_si())+
  theme(legend.position = c(0.93, 0.83),
        legend.title = element_blank(),
        legend.text = element_text(size=8),
        legend.background = element_blank(),
          plot.title.position = "plot",
          axis.title.y = element_text(hjust = 1)
        )
# ----------------------------------------------- line chart frequency of rides
pl2 <- df %>% 
  group_by(user, hour) %>% 
  summarise(n = n()) %>%
  mutate(frq_n = n/sum(n)) %>% 

  ggplot(aes(x = hour, y = frq_n, group = user, color = user)) +
  geom_line(size = 1.5, alpha = 0.5) +
  geom_point(size = 2) +
  scale_color_manual(values = color_table$color) +
  
    labs(title = "",
       subtitle = "Relative frequency",
       caption = "Rel. frequency = n_hour / n_year") +
  
  coord_cartesian(ylim = c(0,0.12)) +
  xlab("hour") +
  ylab("Rel. frequency") +
  scale_y_continuous(labels = scales::label_number_si())+
  theme(legend.position = "none",
          plot.title.position = "plot",
          axis.title.y = element_text(hjust = 1),
          axis.title.x = element_text(hjust = 0)
        )
# ---------------------------------------------------------- display both plots 
# install and load package "gridExtra"
grid.arrange(pl1, pl2, nrow = 2)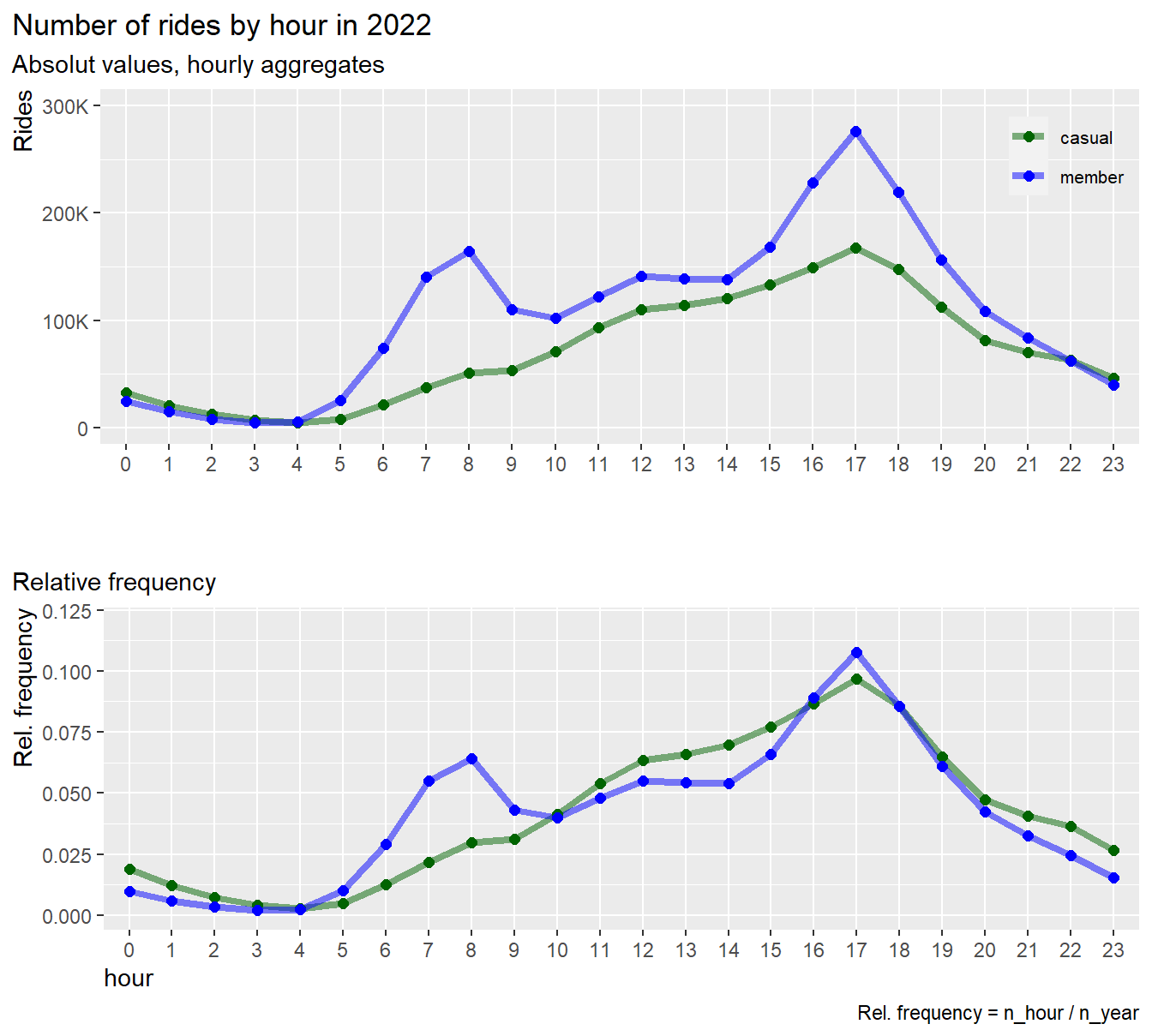

rm(pl1, pl2)

Results:

• The graph shows a substantial difference in ride behavior between members and casuals:
• Members show two relative maximums, one in the morning (8am) and one in the afternoon (5pm), i.e. member use their bikes mainly for commuting
  
• Rides of casuals gradually increases from morning to afternoon (5pm). The graph shows no peak at the morning commute.i.e. casuals seam to use their bikes for other reasons than for commuting
  
  

Average ride-time by hour:

df %>% 
  group_by(user, hour) %>% 
  summarise(avg_rt = round(mean(ride_time),1)) %>%

  ggplot(aes(x = hour, y = avg_rt, group = user, color = user)) +
  geom_line(size = 1.5, alpha = 0.5) +
  geom_point(size = 2) +
  scale_color_manual(values = color_table$color) +
  labs(title = "Average ride-time") +
  
    labs(title = "Average ride-time by hour 2022",
       subtitle = "Hourly aggregates") +
  
  
  coord_cartesian(ylim = c(0,30)) +
  xlab("Hour") +
  ylab("Avg. ride-time (min)") +
  scale_y_continuous(labels = scales::label_number_si())+
  theme(legend.position = c(0.93, 0.17),
        legend.title = element_blank(),
        legend.text = element_text(size=8),
        legend.background = element_blank(),
          plot.title.position = "plot",
          axis.title.y = element_text(hjust = 1),
          axis.title.x = element_text(hjust = 0)
        )

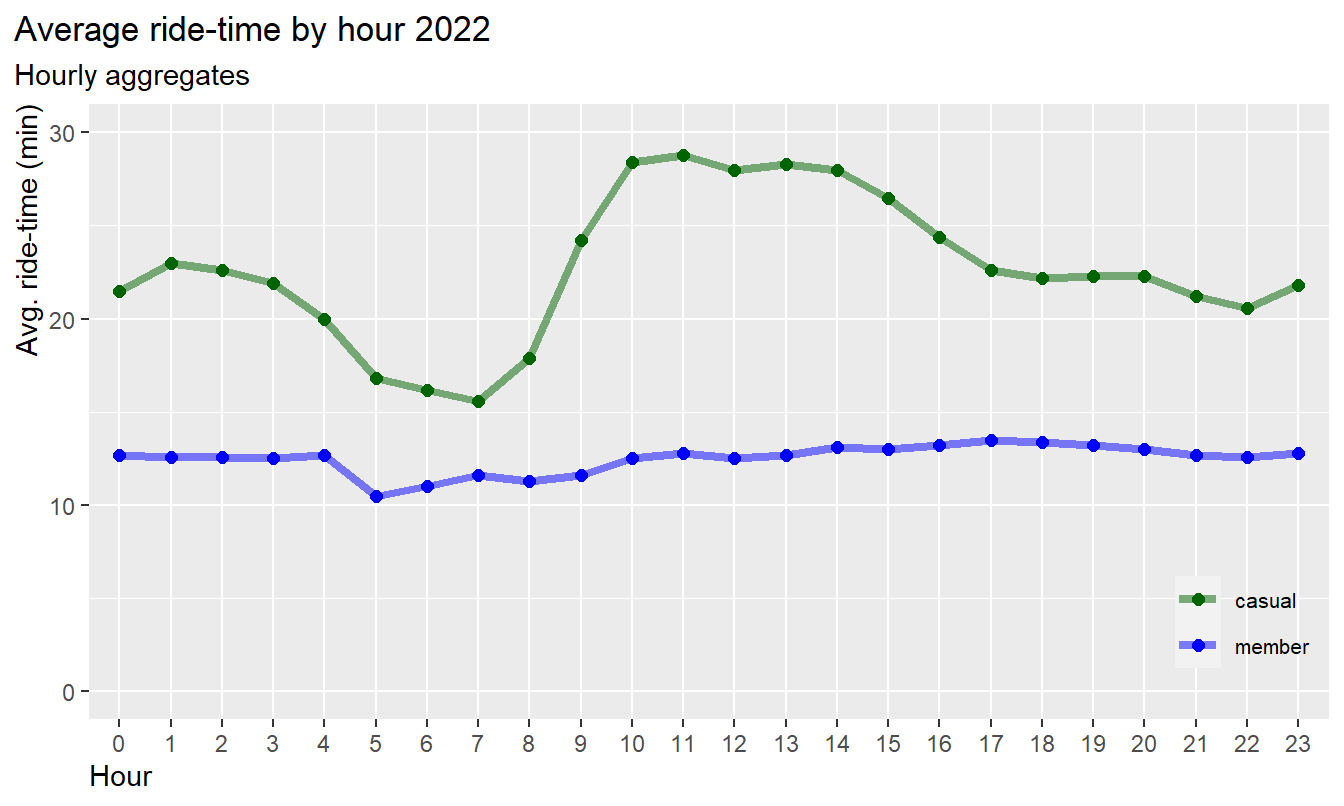
Results:

• The average ride-time of casuals is higher compared to members at all time
  
• The average ride-time of members is almost constant at 13 minutes over the day, i.e. less influenced by the hour
  
• The average ride-time of casuals is longest from 9am to 5pm and lowest from 4am to 8am
  

3.2.5 Conclusions: Time dependencies by month, weekday and hours

Year:

• The number of ride cycle over the year follows the same pattern in both groups, no significant differences due to season can be observed
  
• Both groups show an increase of rides in warmer seasons and decrease in colder seasons
  
• However, casuals show a steeper increase of rides in warmer months, and a drop close to zero in January and February
  
• The average ride time for casuals is increasing in warmer months, highest from March to May
  
• The average ride time of members is almost constant over the year
  

Week:

• Casuals prefer riding on weekends, whereas members ride is highest on workdays
  
• The average ride time of casuals increases on weekends more than for members
  

Day:

• Members prefer riding during commute time in the morning and afternoon hours
  
• Casuals riders, however, show no commute behavior, instead they prefer to ride in the afternoon, assumingly for leisure
  
• The average ride time of casuals is longer during the daytime than at evening and night time
  
• The average ride time of members is constant all over the day
  
  
  

3.3 Usage of bike-types

We will now break down the analysis further by bike-type classic bike and electric bike to get an insight whether there are significant differences between the user groups:

3.3.1 Number of rides (in percentage)

### set color table (global)
color_table_2 <- tibble(
  bike_type = c("classic_bike", "docked_bike", "electric_bike"),
  color = c("#9AC0CD", "#009ACD", "#00688B"))

df %>% 
  group_by(user, bike_type) %>% 
  summarise(n = n()) %>%
  mutate(frq_n = n/sum(n)) %>%   
  
  ggplot(aes(x = user, y = n, fill = bike_type)) +
  geom_bar(stat = "identity", position = "fill")+
  scale_fill_manual(values = color_table_2$color) +
  geom_text(aes(label=paste0(sprintf("%1.1f", frq_n*100), "%")),
            position=position_fill(vjust=0.5), color="white")+  
  labs(title = "Number of rides per bike-type (in percent)") +
  scale_y_continuous(labels = scales::percent) +
  xlab("") +
  ylab("Percent")+
    theme(plot.title.position = "plot",
          legend.title = element_blank(),
          axis.title.y = element_text(hjust = 1)
        )

Results:

• The preferred bike-type in both groups are classic bikes/
• Casuals are more in favor of electric bikes than members (40% against 34%) although the pricing of electric bikes for non-members is $0.42/min and for members is only $0.17/min
  
• The case study does not provide an explanation of docked bikes. Since they are only used by casuals we exclude this type from the further analysis
  
  Let’s look more deeply into the usage of each bike-type by month, week and hour
  
  

3.3.2 Dependency by month and day

Total rides per bike-types aggregated by month for weekend and workday:

df %>% 
  group_by(user, month_name, day_type, bike_type) %>% 
  filter(bike_type != "docked_bike") %>% 
  summarise(n = n()) %>%
  
  ggplot(aes(x = month_name, y = n, group = user, color = user)) +
  geom_line(size = 1.5, alpha = 0.7) +
#  geom_point(size = 2) +
  scale_color_manual(values = color_table$color) +
  

  labs(title = "Number of rides by month for bike-types in 2022",
       subtitle = "Absolut values, monthly aggregates") +

  coord_cartesian(ylim = c(0,200000)) +
  xlab("") +
  ylab("Rides") +
  scale_y_continuous(labels = scales::label_number_si(),
                     breaks = seq(0, 200000, by = 100000))+
  
  facet_grid(bike_type~day_type)+
  theme(legend.position = c(0.08, 0.92),
        legend.title = element_blank(),
        legend.text = element_text(size=8),
        legend.background = element_blank(),
        plot.title.position = "plot", 
        axis.title.y = element_text(hjust = 1)
        )

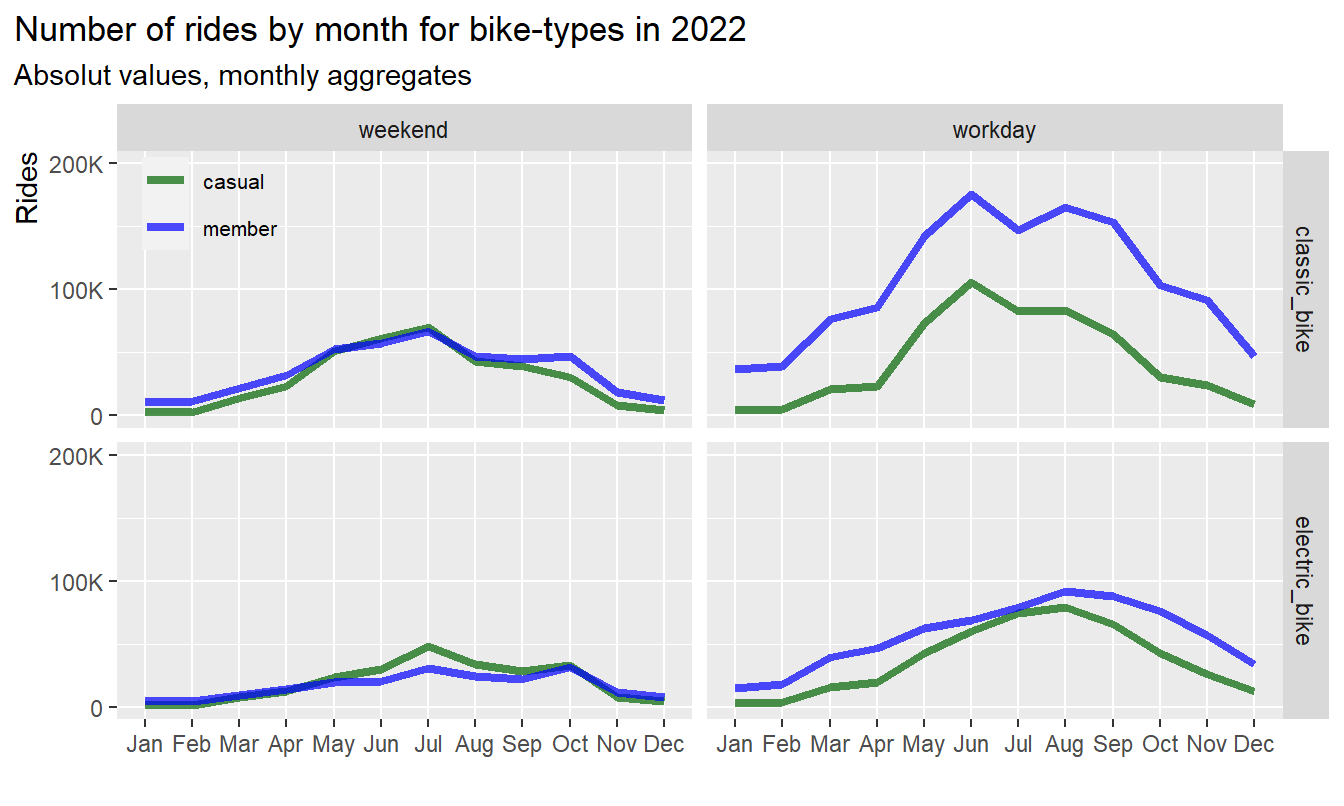
Results:

• On weekends and in summer casuals use more E-bikes than members
  
• On workdays and in summer casuals show an increase usage of E-bikes
  
• The usage of classic bikes follows a similar pattern in both user groups
  
  

3.3.3 Dependency by hour and season (electric bikes)

Total rides of electric bikes aggregated by hour for different seasons at weekend and workday:

df %>% 
  group_by(user, hour, day_type, season) %>% 
  filter(bike_type == "electric_bike") %>% 
  summarise(n = n()) %>%
  
  ggplot(aes(x = hour, y = n, group = user, color = user)) +
  geom_line(size = 1.5, alpha = 0.7) +
#  geom_point(size = 2) +
  scale_color_manual(values = color_table$color) +
  facet_grid(day_type~season, scales = "free_y") +
 
  labs(title = "Number of rides by hour in 2022 (electric bikes)",
       subtitle = "Absolut values, hourly aggregates") +
  
  coord_cartesian(ylim = c(0,30000)) +
  xlab("hour [0 - 23]") +
  ylab("Rides") +
  scale_y_continuous(labels = scales::label_number_si())+
#  scale_x_discrete(guide = guide_axis(check.overlap = TRUE))+
  theme(legend.position = c(0.9, 0.9),
        legend.title = element_blank(),
        legend.text = element_text(size=8),
        legend.background = element_blank(),
          plot.title.position = "plot",
          axis.title.y = element_text(hjust = 1),
          axis.title.x = element_text(hjust = 0),
          axis.text.x = element_blank(),
          axis.ticks.x  = element_blank()
        )

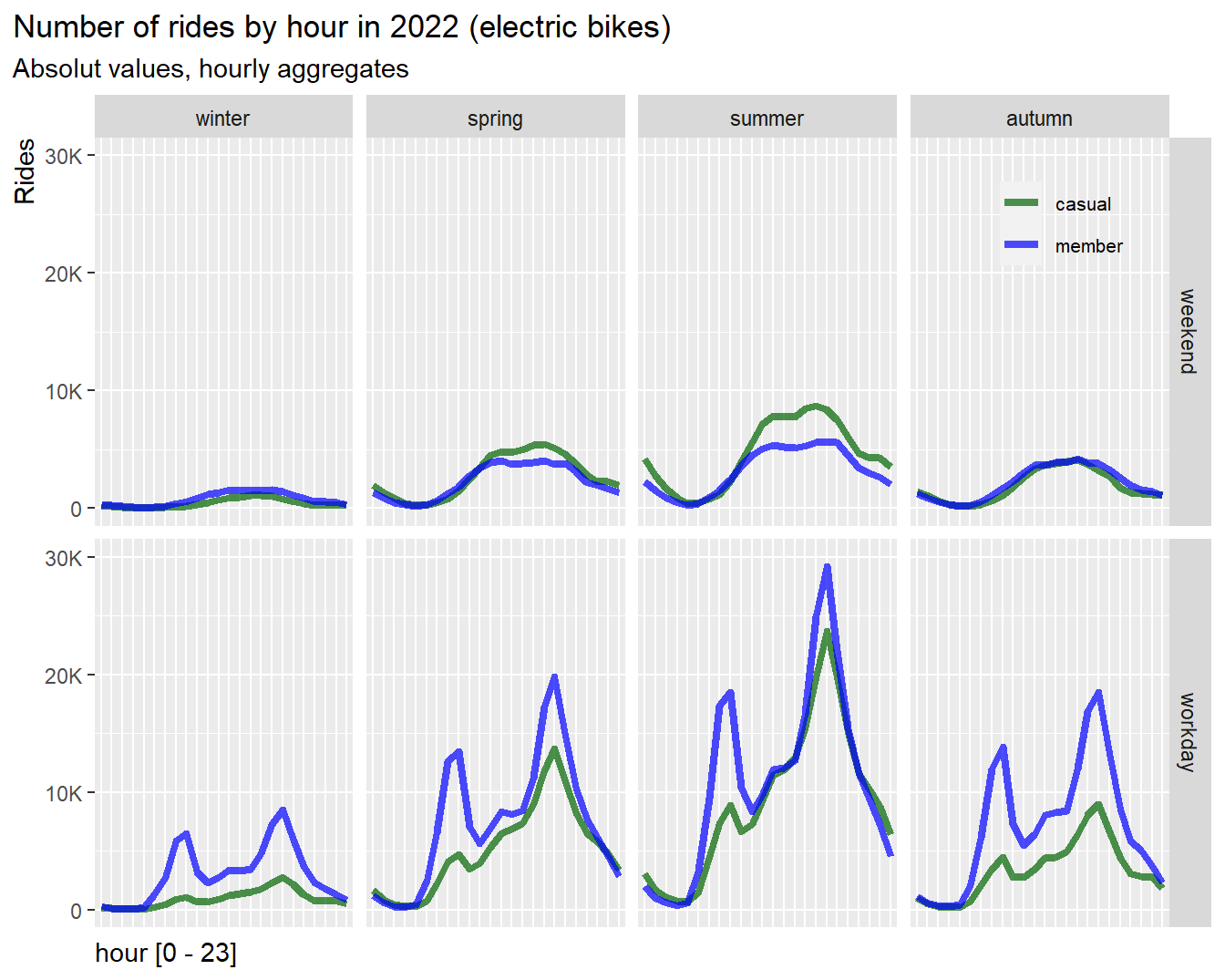
rm(color_table_2)

Results:

• On weekend and in summer casuals use significantly more E-bikes than members
  
• On workdays surprisingly casuals show a slight peak at the morning commute, indicating that a proportion of casual riders use their E-bike for commuting and are potential customers to convert to annual memberships
  
  

3.3.4 Dependency by hour and season (classic bikes)

Total rides of classic bikes aggregated by hour for different seasons, weekend and workday:

df %>% 
  group_by(user, hour, day_type, season) %>% 
  filter(bike_type == "classic_bike") %>% 
  summarise(n = n()) %>%
  
  ggplot(aes(x = hour, y = n, group = user, color = user)) +
  geom_line(size = 1.5, alpha = 0.7) +
#  geom_point(size = 2) +
  scale_color_manual(values = color_table$color) +
  facet_grid(day_type~season, scales = "free_y") +
 
  labs(title = "Number of rides by hour in 2022 (classic bikes)",
       subtitle = "Absolut values, hourly aggregates") +
  
  coord_cartesian(ylim = c(0,30000)) +
  xlab("hour [0 - 23]") +
  ylab("Rides") +
  scale_y_continuous(labels = scales::label_number_si())+
#  scale_x_discrete(guide = guide_axis(check.overlap = TRUE))+
  theme(legend.position = c(0.9, 0.9),
        legend.title = element_blank(),
        legend.text = element_text(size=8),
        legend.background = element_blank(),
          plot.title.position = "plot",
          axis.title.y = element_text(hjust = 1),
          axis.title.x = element_text(hjust = 0),
          axis.text.x = element_blank(),
          axis.ticks.x  = element_blank()
        )

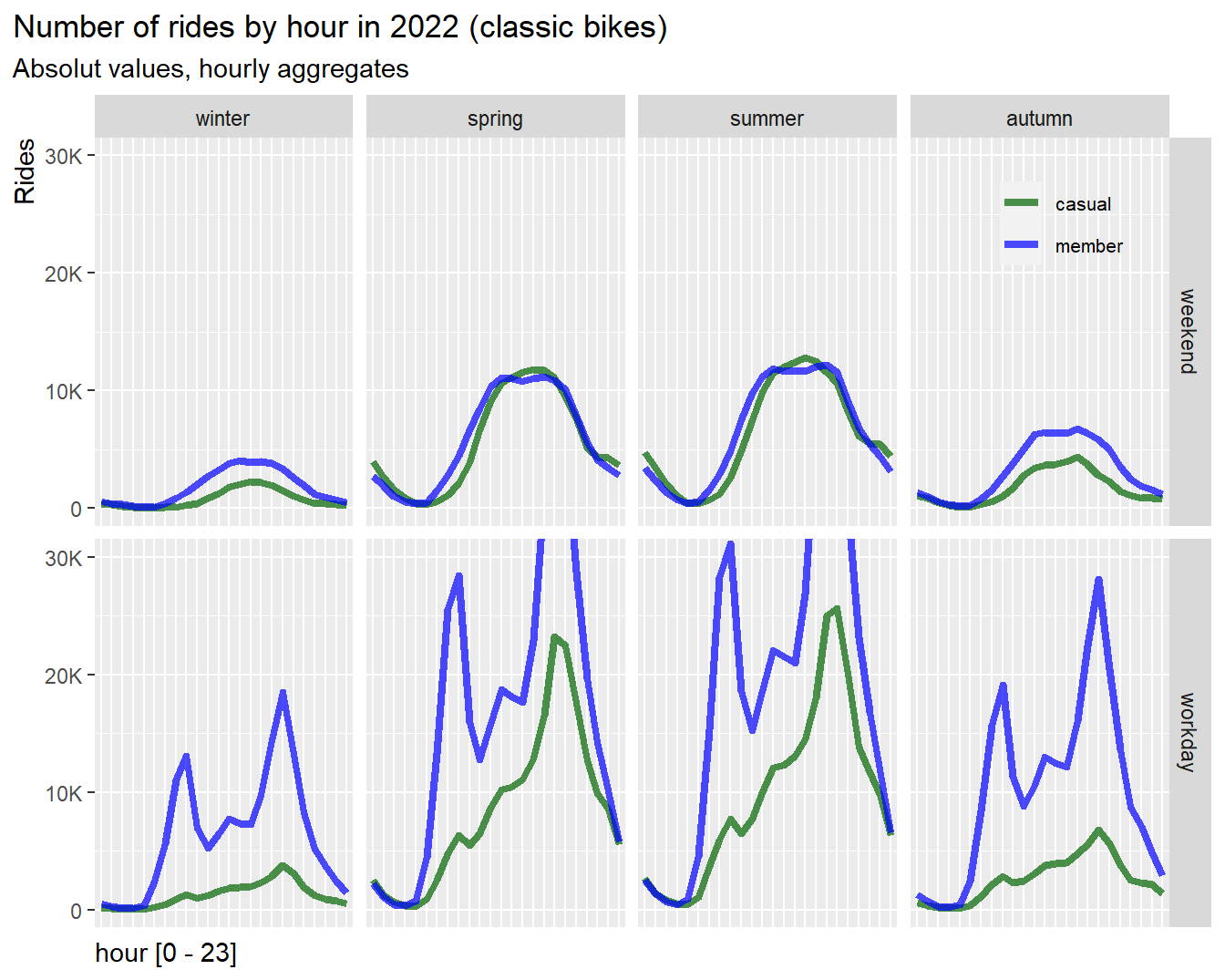
rm(color_table_2)

Results:

• On weekend and in warmer season almost identical usage of classic bikes, but fewer rides by casuals in autumn and winter
  
• On workdays casuals show a tiny peak also in the morning commute but less than electric bike user, indicating that casuals do not use classic bikes much for commuting
  
• In general casuals have high demand of rides in warmer seasons but very low demand in colder seasons
  
  
  

3.3.5 Conclusion: Usage of bike-types

• Casuals are more in favor of electric bikes than members
  
• On summer and spring weekends casuals use more electric bikes than members
  
• Casual use electric bikes to some extend also for morning commute, and may be potential customers for memberships
  
  
  

3.4 Spatial distribution

3.4.1 Top 20 start stations

Next, let’s display the top 20 stations for casuals and members.
For the map visualization we used ggmap and geom_point. The map was pulled from Google Map. A Google Map API is required. We will skip the code here, since the map creation code was quite lengthy. If there is any interest please let me know.

The following maps were created with ggmap and Google Map API:

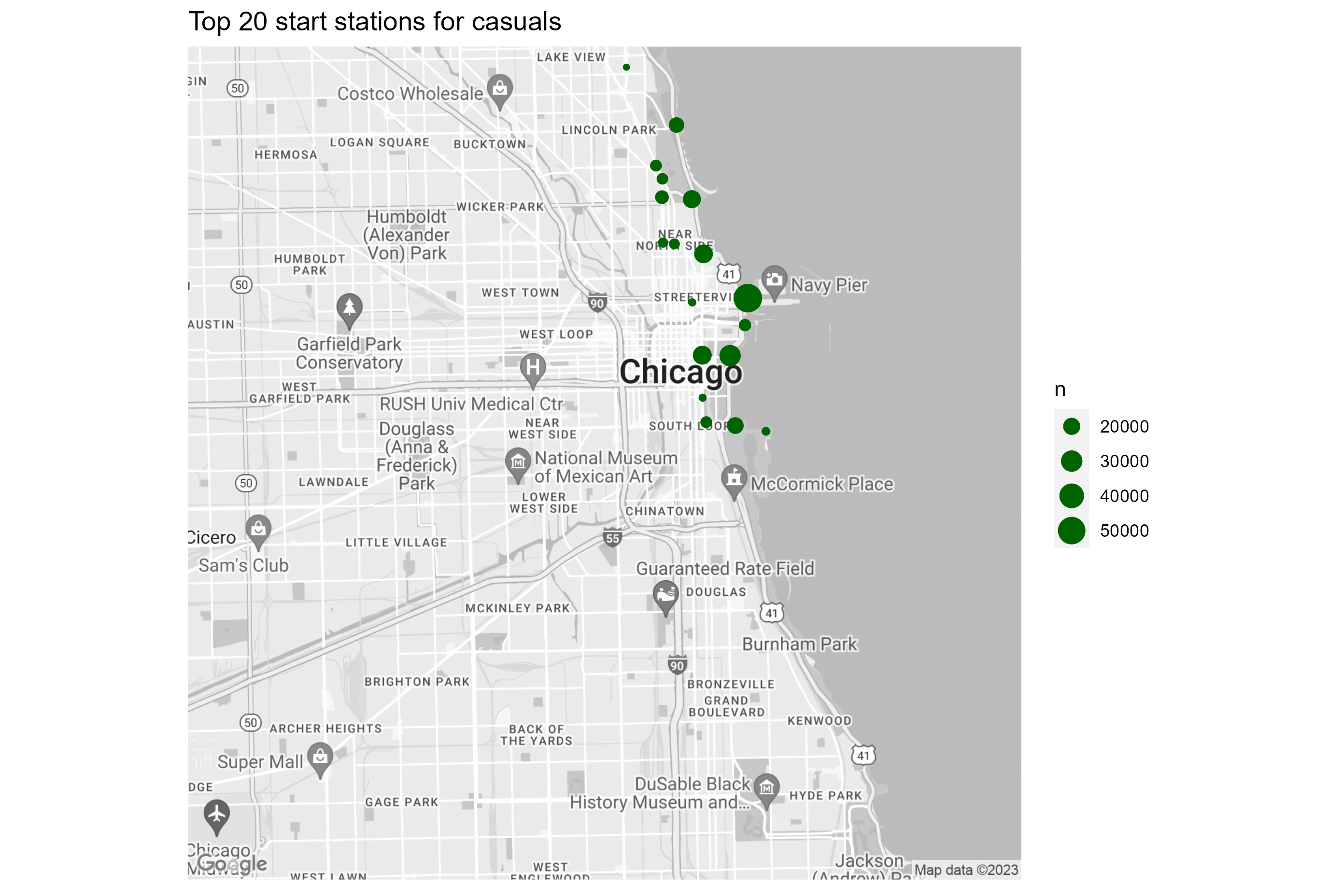
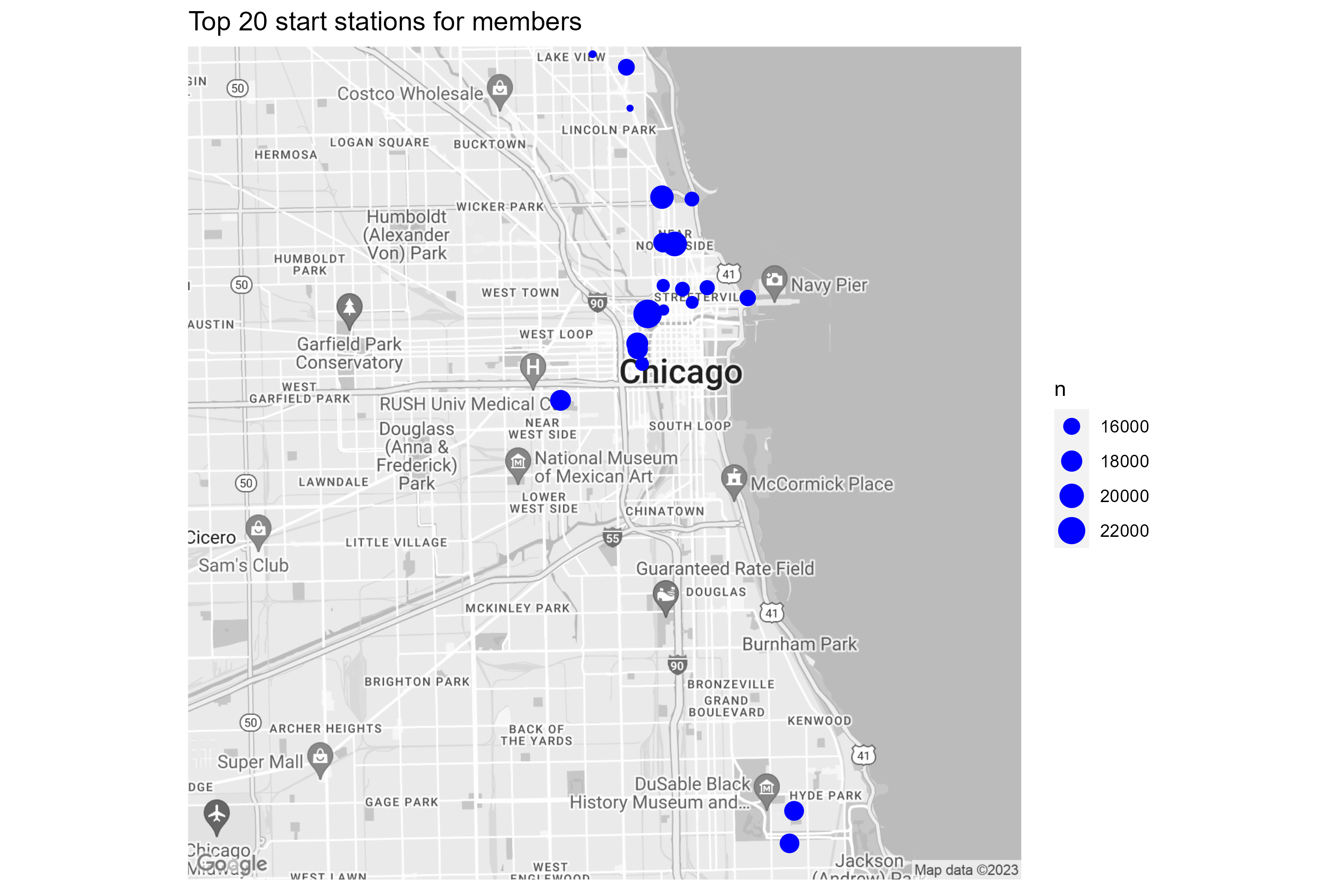
Results:

• Top 20 stations for casuals are concentrated along the lake shore and in park areas. The ride frequency of the top 20 stations ranges from 50K - 20K
  
• Top 20 stations for members are in the city center, business area, and university campuses. The ride frequency of the top 20 station ranges from 22K to 16K, and is more equally distributed compared to casuals
  
  

3.4.2 Density map of rides by location

A density map visualizes the number of rides accumulated over the full time span and mapped to the location of start stations. The range is sliced in 50 levels. Each level is assigned to a color and bounded by a polygon.
For the visualization we used ggmap and stat_density2d function. The map was pulled from Google Map. A Google Map API is required. We will skip the code here, since the map creation code was quite lengthy. If there is any interest please let me know.

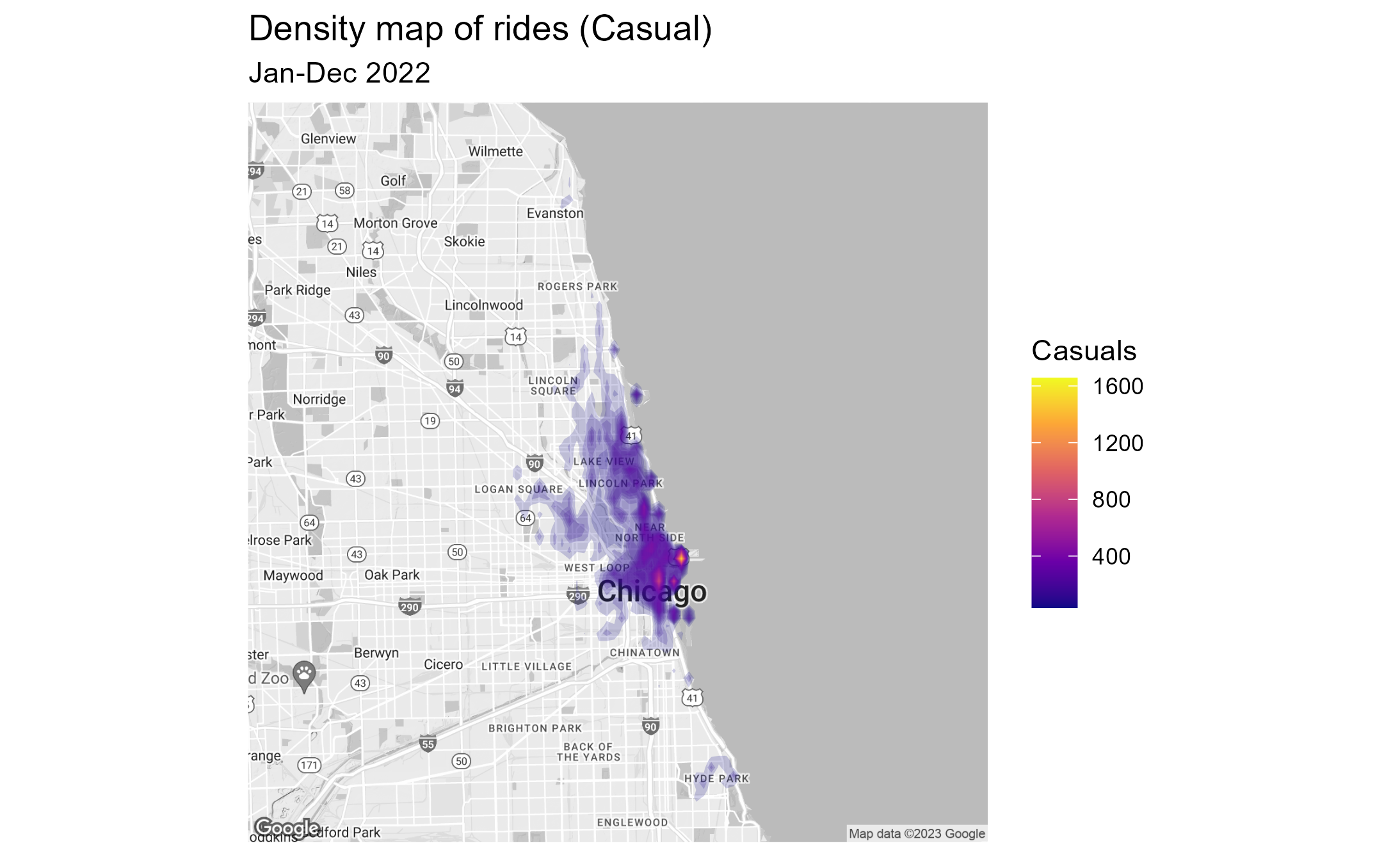
Results:

• Location wise stations used by casual riders are more concentrated in the city and along the lake shore. The frequency range per start station is between 400 and 1600 rides.
  
• Stations used by annual members are much wider spread over greater Chicago area (Evanston to Hide Park). The frequency ranges per start station from 200 to 600 rides and is more equally distributed.
  
  
  

3.4.3 Conclusion: Differences by location

• Casuals have a preference for locations along the lake shore and in park areas
• Members have a preference for locations in the city’s business districts and around university campuses
• Casual riders are more concentrated in the city and along the lake shore, with few hot-spots
  
• Annual members are more wide spread over greater Chicago area
  
  
  

3.5 Modeling

3.5.1 Identify correlations between members and casuals

Relationships (correlations) between casuals and members can be best visualized in scatter plots. We therefore plot the number of rides of casuals on the x-axis and the number of rides of members on the y-axis.

If the groups are correlated, than we can infer that the behavior is not different
If the groups are only weakly correlated, we can infer that a difference in behavior exists

We will then use a simple linear regression model provided by geom_smooth (method = lm). The coefficients of the model are not accessible from geom_smooth. However, we can calculate the R-value with a simple function that provides a measure of correlation (+/- 1 for high correlation and 0 for no correlation). The regression slop values are manually calculated from the graphs.

3.5.2 Prepareing the data set

We will create a new dataframe df_corr to aggregate the number of rides by hour. The data points will be reduced to about 8700 rows

# --------------------------------------------------- select relevant variables

tmp1 <- df %>% 
  mutate(year = year(start_time),
         month = month(start_time),
         day = day(start_time),
         hour = hour(start_time)) %>% 
  mutate(new_time = make_datetime(year, month, day, hour)) %>% 
  select(user, new_time, ride_time, season, day_type, hour_type)

# ---------------------------------------------------- extract subset for casual
tmp_c <- tmp1 %>% 
  filter(user == "casual") %>% 
  group_by(new_time) %>% 
  summarise(rides_casual = n(), 
            ride_time_casual = sum(ride_time),
            avg_ride_time_casual = mean(ride_time),
            season,
            day_type,
            hour_type) %>% 
  distinct()

# ---------------------------------------------------- extract subset for member
tmp_m <- tmp1 %>% 
  filter(user == "member") %>% 
  group_by(new_time) %>% 
  summarise(rides_member = n(), 
            ride_time_member = sum(ride_time),
            avg_ride_time_member = mean(ride_time),
            season,
            day_type,
            hour_type) %>% 
  distinct()

# ----------------------------------------------------------------- Join subsets
df_corr <- tmp_c %>% 
  inner_join(tmp_m)

# --------------------------------------------------------------------- Clean up
rm(tmp1, tmp_c, tmp_m)

3.5.3 Overall correlation

# ------------------------------------------------------------- Correlation test
corr <- cor.test(df_corr$rides_casual, df_corr$rides_member)
# print(corr)

# ----------------------------------------------------------------- scatter plot
df_corr %>% 
  select(new_time, rides_casual, rides_member) %>%
  
  ggplot(aes(x = rides_casual, y = rides_member))+
  geom_point(alpha = 0.2)+
    geom_smooth(se = TRUE, method = lm)+
  labs(title = "Relationship between rides casual and rides member",
       subtitle = "Each data point is an hourly aggregate") +
  xlab("Number of rides (casual)")+
  ylab("Number of rides (member)")+
#  scale_y_continuous(labels = scales::label_number_si())+
#  scale_x_continuous(labels = scales::label_number_si())+
  annotate("text", x=90, y=1550, label=paste("R = ", round(corr$estimate, 2)), size = 4)+
  theme(plot.title.position = "plot",
        axis.title.y = element_text(hjust = 1),
        axis.title.x = element_text(hjust = 0))

rm(corr)

Result: 

• The number of rides for casuals and members are correlated by R = 0.8
  
• The slope of the regression line is about 1:0.9, but we can observe a large spread the farther we move out on the axis

To find some further clues we will look into correlation by season, weekdays and hour

3.5.4 Correlations by seasons

Now let’s split the data in rides by season. The seasons are defined as:

• winter: Jan, Feb, Mar
  
• spring: Apr, May, Jun
  
• summer: Jul, Aug, Sep
  
• autumn: Oct, Nov, Dec
  

# R coefficient for "winter"
df_corr_winter <- df_corr %>% 
  filter(season == "winter")
corr_winter <-  cor.test(df_corr_winter$rides_casual, df_corr_winter$rides_member)

# R coefficient for "spring"
df_corr_spring <- df_corr %>% 
  filter(season == "spring")
corr_spring <-  cor.test(df_corr_spring$rides_casual, df_corr_spring$rides_member)

# R coefficient for "summer"
df_corr_summer <- df_corr %>% 
  filter(season == "summer")
corr_summer <-  cor.test(df_corr_summer$rides_casual, df_corr_summer$rides_member)

# R coefficient for "autumn"
df_corr_autumn <- df_corr %>% 
  filter(season == "autumn")
corr_autumn <-  cor.test(df_corr_autumn$rides_casual, df_corr_autumn$rides_member)

# create annotation fields
dat_text <- data.frame(
  label = c(paste("R = ", round(corr_winter$estimate, 2)),
            paste("R = ", round(corr_spring$estimate, 2)),
            paste("R = ", round(corr_summer$estimate, 2)),
            paste("R = ", round(corr_autumn$estimate, 2))),
  season = c("winter", "spring","summer", "autumn")
  )
dat_text$season <- factor(dat_text$season, ordered = TRUE)
dat_text$season <- fct_relevel(dat_text$season,
                               "winter",
                               "spring",
                               "summer",
                               "autumn")

# scatter plot - season
df_corr %>% 
  select(new_time, rides_casual, rides_member, season) %>%
  
  ggplot(aes(x = rides_casual, y = rides_member))+
  geom_point(color = "black", alpha = 0.1)+
  geom_smooth(method = "lm")+
  labs(title = "Correlation between casual and member by season",
       subtitle = "Each data point is an hourly aggregate") +
  xlab("Rides per hour (casual)")+
  ylab("Rides per hour (member)")+
  facet_wrap(~season, ncol = 2)+
  geom_text(
    data = dat_text,
    mapping = aes(x = -Inf, y = -Inf, label = label),
    size = 3,
    hjust = -0.2,
    vjust = -27,
    check_overlap = TRUE)+
  theme(plot.title.position = "plot",
        axis.title.y = element_text(hjust = 1),
        axis.title.x = element_text(hjust = 0))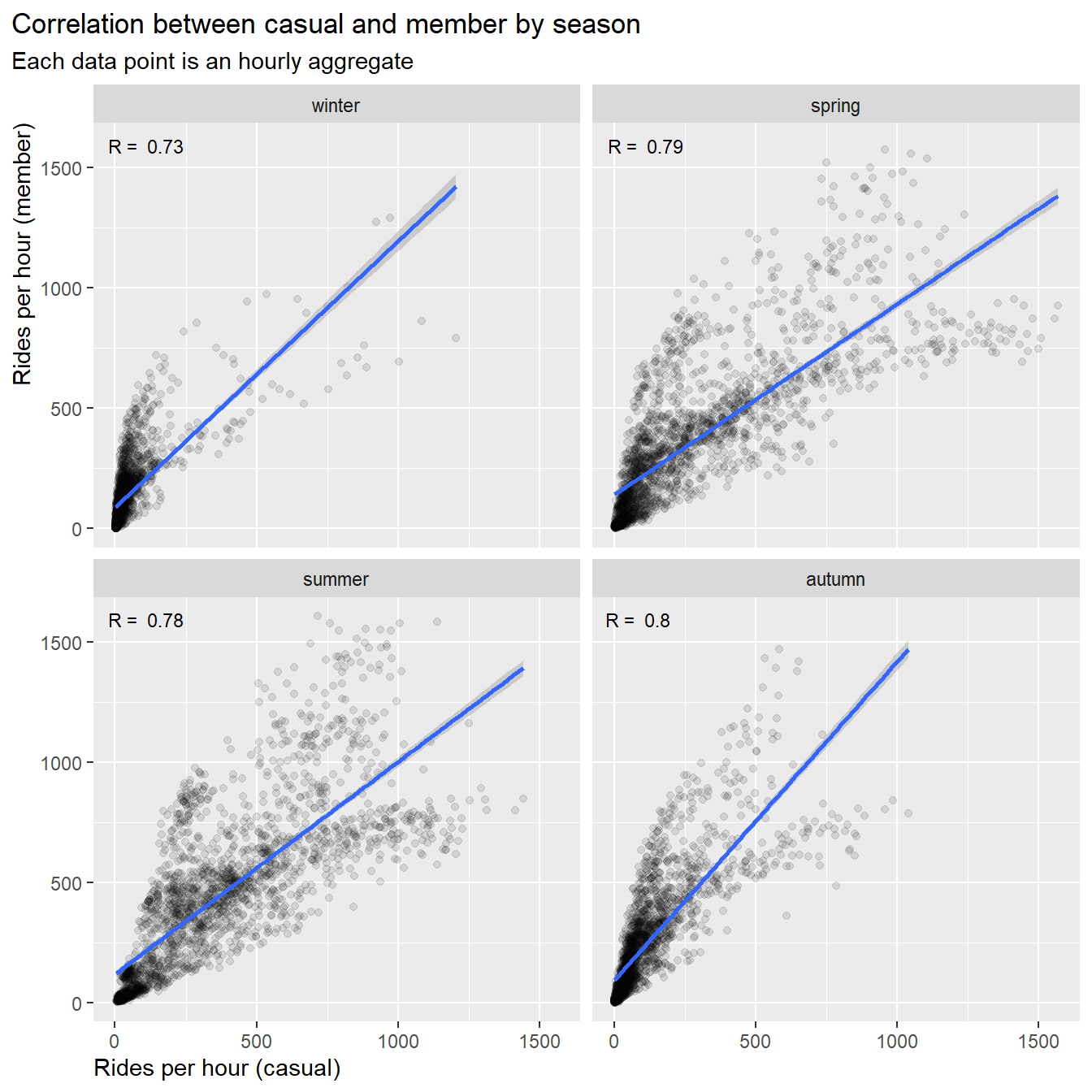

# Cleaning up
rm(df_corr_winter, df_corr_spring, df_corr_summer, df_corr_autumn, 
   corr_autumn, corr_spring, corr_summer, corr_winter, dat_text)

Result:

• The correlation values for all seasons are between R = 0.7 ~ 0.8, we can’t specify differences between casuals and members due to seasons
  
• The slopes are a little steeper for winter (1:1.2) and autumn (1:1.3), i.e. trend to more rides by members than by casuals
  
• The slopes for summer are close to 1:1, summer (1:0.8) and spring (1:0.9), i.e. trend to equal number of rides for members and casuals
  
  

3.5.5 Correlations by weekday

Next let’s split the data in rides by day-type. The day-types are defined as:

• weekend: Sat, Sun
  
• workday: Mon, Tue, Wed, Thu, Fri
  

# R coefficient for "weekend"
df_corr_we <- df_corr %>% 
  filter(day_type == "weekend")
corr_we <-  cor.test(df_corr_we$rides_casual, df_corr_we$rides_member)

# R coefficient for "workday"
df_corr_wd <- df_corr %>% 
  filter(day_type == "workday")
corr_wd <-  cor.test(df_corr_wd$rides_casual, df_corr_wd$rides_member)

# create annotation fields
dat_text <- data.frame(
  label = c(paste("R = ", round(corr_we$estimate, 2)),
            paste("R = ", round(corr_wd$estimate, 2))),
  day_type = c("weekend", "workday")
)
dat_text$day_type <- factor(dat_text$day_type, ordered = TRUE)


# scatter plot
df_corr %>% 
  select(new_time, rides_casual, rides_member, day_type) %>%
  
  ggplot(aes(x = rides_casual, y = rides_member))+
  geom_point(color = "black", alpha = 0.2)+
  geom_smooth(method = "lm")+
  labs(title = "Correlation between casual and member by weekday",
       subtitle = "Each data point is an hourly aggregate") +
  xlab("Rides per hour (casual)")+
  ylab("Rides per hour (member)")+
  geom_text(
    data = dat_text,
    mapping = aes(x = -Inf, y = -Inf, label = label),
    size = 3,
    hjust = -0.1,
    vjust = -32)+
  theme(plot.title.position = "plot",
        axis.title.y = element_text(hjust = 1),
        axis.title.x = element_text(hjust = 0))+
  facet_wrap(~day_type)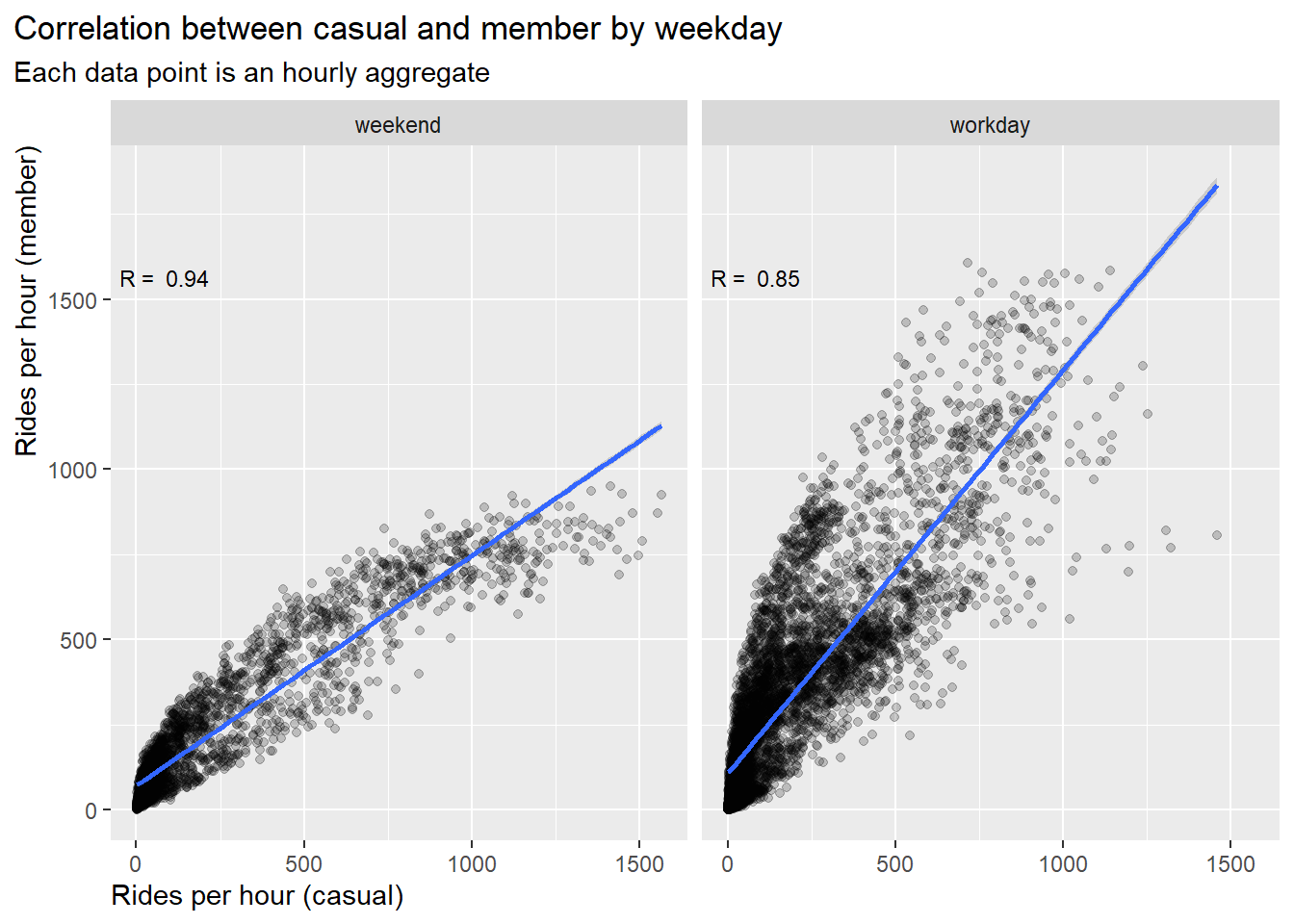  

# cleaning up
rm(df_corr_we, df_corr_wd, corr_we, corr_wd, dat_text)

Result: 

• The correlation on weekend (R=0.94) is stronger than on workdays (R=0.85), i.e. ride behavior on workdays shows more differences between the user groups
  
• The slop on weekends is 1:0.7, i.e. trend to more casuals than members
  
• The slop on workdays is 1:1.2, i.e. trend to more members than casuals
  
  

3.5.6 Correlation by day time

Finally let’s split the data in rides by day time. The day times is defined as:

• night : 00:01 - 06:00
  
• morning : 06:01 - 12:00 (morning commute)
  
• afternoon : 12:01 - 18:00 (afternoon commute)
  
• evening : 18:01 - 00:00
  
  

# R coefficient for "night"
df_corr_night <- df_corr %>% 
  filter(hour_type == "night")
corr_night <-  cor.test(df_corr_night$rides_casual, df_corr_night$rides_member)

# R coefficient for "morning"
df_corr_morning <- df_corr %>% 
  filter(hour_type == "morning")
corr_morning <-  cor.test(df_corr_morning$rides_casual, df_corr_morning$rides_member)

# R coefficient for "afternoon"
df_corr_afternoon <- df_corr %>% 
  filter(hour_type == "afternoon")
corr_afternoon <-  cor.test(df_corr_afternoon$rides_casual, df_corr_afternoon$rides_member)

# R coefficient for "evening"
df_corr_evening <- df_corr %>% 
  filter(hour_type == "evening")
corr_evening <-  cor.test(df_corr_evening$rides_casual, df_corr_evening$rides_member)

# create annotation fields
dat_text <- data.frame(
  label = c(paste("R = ", round(corr_night$estimate, 2)),
            paste("R = ", round(corr_morning$estimate, 2)),
            paste("R = ", round(corr_afternoon$estimate, 2)),
            paste("R = ", round(corr_evening$estimate, 2))),
  hour_type = c("night", "morning","afternoon", "evening")
)
dat_text$hour_type <- factor(dat_text$hour_type, ordered = TRUE)


# scatter plot
df_corr %>% 
  select(new_time, rides_casual, rides_member, hour_type) %>%
  
  ggplot(aes(x = rides_casual, y = rides_member))+
  geom_point(color = "black", alpha = 0.1)+
  geom_smooth(method = "lm")+
  labs(title = "Correlation between casual and member by day time",
       subtitle = "Each data point is an hourly aggregate") +
  xlab("Rides per hour (casual)")+
  ylab("Rides per hour (member)")+
  facet_wrap(~hour_type, ncol = 2)+
  geom_text(
    data = dat_text,
    mapping = aes(x = -Inf, y = -Inf, label = label),
    size = 3,
    hjust = -0.2,
    vjust = -27,
    check_overlap = TRUE)+
  theme(plot.title.position = "plot",
        axis.title.y = element_text(hjust = 1),
        axis.title.x = element_text(hjust = 0))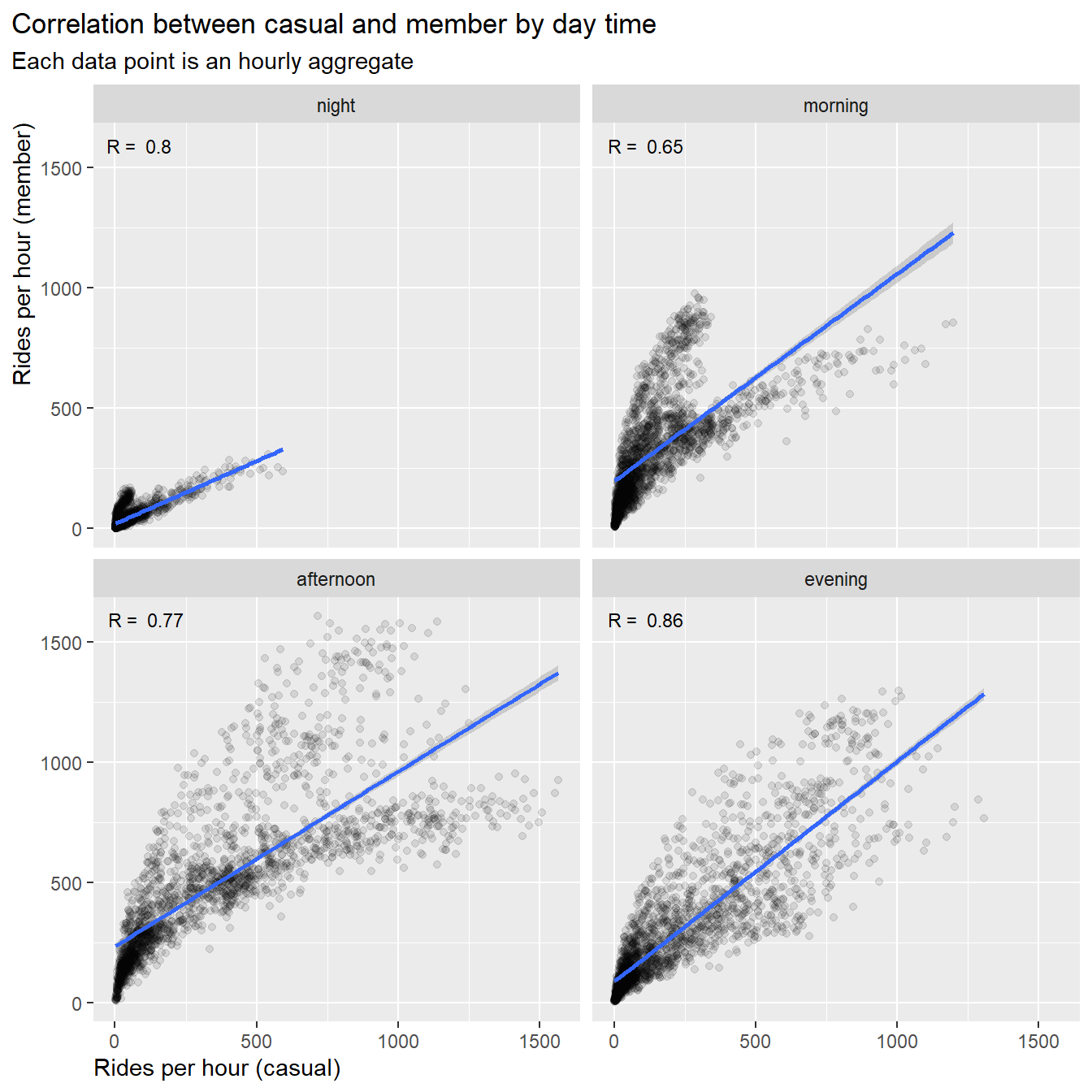

# Cleaning up
rm(df_corr_night, df_corr_evening, df_corr_morning, df_corr_afternoon,
   corr_night, corr_morning, corr_evening, corr_afternoon, dat_text)

Results: 

• The correlation in the morning hours is weak (R=0.65), i.e.in the morning hours we can observe more differences in ride behavior between casuals and members
  
• The correlations in the afternoon, evening and night hours is about R=0.8 and correlated
  
• The slops for morning hours and evening hours is 1:0.9, i.e. trend to equal number of members and casuals
  
• The slop for afternoon hours is 1:0.8, i.e. trend to more casual rides
  
• The slop for night hours is flat (1:0.5), i.e. trend to more casual rides
  
  

3.5.7 Conclusions for correlation between casuals and members

The relationship of ride numbers between casual and member user were analyzed by simple linear regression models segmented into season, weekdays and hours. All models were significant (very small p-values): The models verify our findings from the time series in chapter 3.2:

• There are no significant difference of user behavior related to season
  
• The ride behavior on workdays shows more difference between the user groups
  
• In the morning hours a clear difference in ride behavior between casuals and members can be observed
  
  
  

4. Answer the question

How do annual members and casual riders use Cyclistic bikes differently?

4.1 Differences between users

Overall:

• Annual members ride more than casual riders over the year
  
• Casual riders accumulate more ride time over the year
  
• The median ride-time of casual riders is longer
  
  

By months:

• Both groups show an increase of rides in warmer season and decrease in colder season
  
• However, in case of casual riders the change is more extreme, i.e. more rides in summer and only very few rides in winter
  

By week:

• Casuals prefer riding on weekends and for longer time
  
• Members prefer riding on workdays, their ride-time is constant over the week
  
  

By day:

• Members prefer riding during commute time in the morning and afternoon hours, indicating that member use their bikes primarily for commuting
  
• Casuals use their bikes primarily in the afternoon, indicating that they use it more for leisure activities
  
  

By bike type:

• Casuals favor electric bikes more than members
  
• On summer weekends casuals use more electric bikes than members
  
• Casuals use electric bike to some extend also for the morning commute, indicating that a portion of casual riders could be interested in a membership with a seasonal pass
  
  

By location:

• Casuals have a preference for locations along the lake shore, in park areas and in the city
  
• Members use station all over greater Chicago area with a concentration in the city’s business districts and on university campuses
  
  
  

4.2 Recommendations:

Scenario 1: Introduction of Seasonal Memberships

• Casual riders show a distinct ride preference from June to September and on weekends.
  
• Therefore, we recommend the introduction of seasonal passes for the warmer season and for weekends.
  
  

Scenario 2: Introduction of Benefit Program for Electric Bikes

• Casual riders prefer to use more electric bikes than members. A smaller but significant portion of casual riders use electric bikes during the morning commute hours. They might be interested in attractive programs targeting especially electric bikes. This could be combined with seasonal membership to attract more casual riders.
  
  

Scenario 3: Convert Casual Riders to Annual Memberships

• Since casuals’ ride pattern distinctively differs from those of members, it will be difficult to convert casual rider into members even with extensive promotion programs. We therefore do not recommend this path.
  
  
  

Thank you for your interest !